In our previous post , Correspondence Analysis: What is it, and how can I use it to measure my brand? (Part 1 of 2), we discussed the uses and benefits of correspondence analysis, and walked through the set up and calculations for correspondence analysis, culminating with creating our first standard correspondence analysis plot (shown below). In this post, we’ll dive deeper into different variations of correspondence analysis that could prove more helpful for our brand perception needs.

Row/column principal correspondence analysis

Standard correspondence analysis is easy to calculate, and strong results can be drawn from it. However, standard correspondence is a poor choice for our needs; the distances between row and column coordinates are exaggerated, and there isn’t a straightforward interpretation of relationships between row and column categories. What we want for interpreting relationships between row(brand) coordinates, and interpreting relationships between row and column categories, is row principal normalization (or, if our brands were on our columns, column principal normalization).

For row principal normalization, you want to utilize the standard coordinates calculated above for your column (attribute) values, but you want to calculate the principal coordinates for your row (brand) values. Calculating the principal coordinates is as simple as taking the standard coordinates, and multiplying them by their corresponding singular values(d). So for our rows, we just want to multiply our standard row coordinates by our singular values(d), shown in the table below. For column principal normalization we would simply multiply our columns instead of our rows by our singular values(d).

Substituting in our principal coordinates for our rows(brands), we end up with:

Because we scaled by our singular values, our principal coordinates for our rows represent the distance between the row profiles of our original table; one can interpret the relationships between our row coordinates in our correspondence analysis chart by their proximity to one another.

The distance between our column coordinates, since they are based on standard coordinates, are exaggerated still. Also, our scaling by our singular values in just one of the two categories(rows/columns) has given us a way of interpreting relationships between row and column categories. Given a row value and a column value, for example, Butterbeer(row), and Tasty(column), the longer their distance to the origin, the stronger their association with other points on the map. Also, the smaller the angle between the two points (Butterbeer and Tasty), the higher the correlation between the two.

The distance to origin combined with the angle between the two points is the equivalent of taking the dot product; the dot product between a row and column value measures the strength of the association between the two. In fact, when the first and second dimension explain all of the variance in the data (add up to 100%), the dot product is directly equal to the indexed residual of the two categories. Here, the dot product would be the distance to origin of the two points multiplied by the cosine of the angle between them; .59*2.12*cos(41) = .94. Taking into account rounding errors, it is the same as our indexed residual value of .95. Thus, angles smaller than 90 degrees represent a positive indexed residual and thus a positive association, and angles larger than 90 degrees represent a negative indexed residual or negative association.

Scaled row principal correspondence analysis

Looking at our chart above for row principal normalization, we have an easy observation - the points for our columns (traits) are much more spread out, and our points for our rows (brands) are clustered around the origin. This can make analyzing our graph by eye rather difficult and unintuitive, and sometimes impossible to read the row categories if they’re all overlapping. Luckily, there is an easy way to scale our graph to bring in our columns, while still keeping the ability to utilize the dot product (distance from origin and angle between points) to analyze the relationships between our row and column points, known as scaled row principal normalization.

Scaled row principal normalization takes row principal normalization, and scales the column coordinates the same way we scaled the x-axis of the row coordinates - in other words, our column coordinates are scaled by the first value of our singular values(d). Our row values stay the same as row principal normalization, but now our column coordinates are scaled down by a constant factor.

What this means for us is that our column coordinates are scaled to fit much better with our row coordinates, making it much easier to analyze trends. Because we scaled all our column coordinates by the same constant factor, we contracted the scatter of our column coordinates on the map, but made no change to their relativities; we still utilize the dot product to measure the strength of associations. The only change is that when our first and second dimension cover all of the variance in the data, instead of the indexed residual being equal to the dot product of the two categories, it’s now equal to the scaled dot product of the two categories, which is the dot product scaled by a constant value of our first singular value(d). Interpretation of the chart stays the same as row principal normalization.

Principal correspondence analysis

A final form of correspondence analysis that we will mention is principal correspondence analysis, also known as symmetric map, french scaling, or canonical correspondence analysis. Instead of only multiplying the standard rows or columns by the singular values(d) as in row/column principal correspondence analysis, we multiply both of them by the singular values. So our standard column values, multiplied by the singular values, become:

Putting these together with our row values calculated in row principal analysis, we get:

Canonical correspondence analysis scales both the row and column coordinates by the singular values. What this means is that we can interpret our relationships between our row coordinates just like how we did in row principal correspondence analysis (based on proximity), AND we can interpret our relationships between our column coordinates similarly to column principal correspondence analysis; we can analyze relationships between brands and relationships between attributes. We also lose the row/column clustering in the center of the map from row/column principal analysis. However, what we lose from canonical correspondence analysis, is a way of interpreting relationships between our brands and attributes, something very useful in brand perceptions.

Side-by-side Comparison

Standard Correspondence Analysis

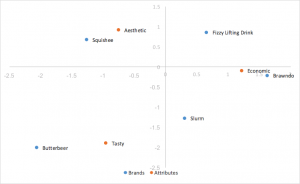
The easiest style of correspondence analysis to compute, using left and right singular vectors of SVD divided by row and column masses. The distances between row and column coordinates are exaggerated, and there isn’t a straightforward interpretation of relationships between row and column categories.

Row Principal Normalization Correspondence Analysis

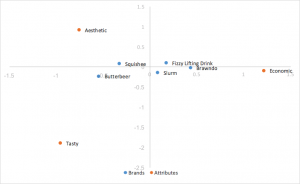
Uses standard coordinates from above, but multiplies the row coordinates by the singular values to normalize. Relationships between rows (brands) is based on distance from one another. Column (attribute) distances are exaggerated still. Relationships between rows and columns can be interpreted by the dot product. Rows (brands) tend to be clumped in the center.

Scaled Row Principal Normalization Correspondence Analysis

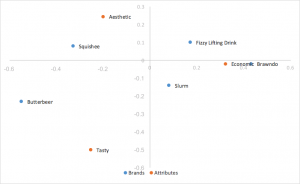
Takes row principal normalization and scales column coordinates by a constant of the first singular value. Same interpretations drawn as row principal normalization, replacing dot product with scaled dot product. Helps remove clumping of rows in the center. This is the style of correspondence analysis which we prefer.

Principal Normalization Correspondence Analysis (Symmetrical, French Map, Canonical)

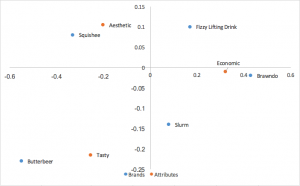
Another popular form of correspondence analysis using principal normalized coordinates in both the rows and columns. Relationships between rows (brands) can be interpreted by distance to one another; the same can be said for columns (attributes). No interpretation can be drawn for relationships between rows and columns.

Wrapping Up

In conclusion, correspondence analysis is used to analyze the relative relationships between and within two groups; in our case, these groups would be brands and attributes.

Correspondence analysis eliminates a skew in results from different masses between groups by utilizing indexed residuals. For brand perceptions for correspondence analysis, we utilize row principal (or column principal if the brands are placed on the columns) normalization, as this allows us to analyze relationships between different brands by their proximity to one another, and also allows us to analyze relationships between brands and attributes by their distance from the origin combined with the angle between them and the origin (the dot product), at the sacrifice of misrepresenting the relationship between attributes with exaggerated distances (which doesn’t matter to us as we don’t care about the relationships between attributes). We utilize the scaled row/column principal normalization to make it easier to analyze our graph at no cost. We want to make sure to keep in mind that we add up the variance explained from the X and Y axis labels (the first and second dimension) to view the total variance captured in the map; the lower this number is, the more unexplained variance there is in the data, and the more misleading the plot.

A last thing to remember is that correspondence analysis only shows relativities since we eliminated the mass factor of our data; our graph will tell us nothing about which brands have the ‘highest’ scores in attributes. Once you understand how to create and analyze the graphs, correspondence analysis is a powerful tool that disregards brand sizing effects to deliver powerful and easy to interpret insights about relationships both between and within brands and their applicable attributes.