Was ist eine Faktorenanalyse?
Eine Faktorenanalyse ist eine Methode, um Daten auszuwerten, indem zahlreiche Variablen auf nur wenige relevante Faktoren reduziert werden. Sie gehört zu den struktur-entdeckenden Verfahren und findet vor allem im Rahmen von Positionierungsanalysen Verwendung. Weiterhin kann die Reduktion der Variablenanzahl entweder durch die konfirmatorische oder die explorative Faktorenanalyse vonstattengehen:
- Die konfirmatorische Faktorenanalyse ist hypothesengeleitet – sie prüft, ob vorher theoretisch festgelegte Modelle zu der Faktorenverteilung tatsächlich so eingesetzt werden können.
- Die explorative Faktorenanalyse geht hingegen explorativ und mathematisch vor. Es wird demnach untersucht, wie gut jede einzelne Variable zu den verschiedenen Faktoren passt, bevor diese zugeteilt werden.
Welchen Vorteil hat eine Faktorenanalyse?
Durch die Faktorenanalyse lassen sich mehrere Variablen zu aussagekräftigen Faktoren zusammenfassen, wie beispielsweise „Qualität“ oder „Nutzen“.
So wird die Datengrundlage sehr viel übersichtlicher und strukturierter – da klar ist, wie die einzelnen Variablen zusammenhängen und welche davon unabhängig voneinander zur Fragestellung beitragen.
Außerdem lassen sich mithilfe der Faktorenanalyse Antworten-Cluster bei Marktstudien aufdecken. Anstatt eine Vielzahl von ähnlichen Variablen auszuwerten, können sich Marketer auf die wichtigsten Themen konzentrieren – und den analytischen Nutzen somit vergrößern.
Unterschied konfirmatorische und explorative Faktorenanalyse
Bei der konfirmatorischen Faktorenanalyse gibt es bereits ein konkretes Modell der möglichen Faktoren. Die Analyse dient hier der Validierung der vorgegebenen Faktorenstruktur. Es soll beantwortet werden, ob das Modell mit den vorhandenen Daten konsistent ist. Zu diesem Zweck folgt die konfirmatorische Faktorenanalyse folgenden Schritten:
- Modellspezifikation
- Parameterschätzung
- Modellbeurteilung
- ggf. Modellmodifikation
Bei der explorativen Faktorenanalyse geht es darum, die Zusammenhänge sowie die vorab unbekannten Strukturen zwischen den Variablen aufzudecken. Die Anzahl der zu extrahierenden Faktoren sowie deren inhaltliche Bedeutung ist vor der Analyse unbekannt. Die explorative Faktorenanalyse hat die Komplexitätsreduktion zum Ziel.
Im weiteren Verlauf wird es um die explorative Faktorenanalyse gehen.
Zielkonflikt der Faktorenanalyse
Der Zielkonflikt der Faktorenanalyse besteht darin zu wählen, ob eine hohe oder eine geringe Faktorenanzahl zielführender ist.
| Hohe Faktorenanzahl | Geringe Faktorenanzahl |
|---|---|
|
|
|
|
|
|
Da beide Vorgehensweisen Vor- und Nachteile mit sich bringen, muss für jede Fragestellung einzeln entschieden werden, welches Verfahren sich besser eignet.
Vorgehen bei einer Faktorenanalyse
Die Durchführung einer explorativen Faktorenanalyse beinhaltet mehrere Schritte. Dabei geht es nicht nur darum zu bestimmen, welche Faktorenanzahl angemessen ist, sondern auch, welche Variablen angewendet werden sollen.
Auswahl der Variablen und Erstellung der Korrelationsmatrix
Zunächst gilt es die einzelnen Variablen auszuwählen. Dafür sollte vorab eine Korrelationsmatrix für alle zu berücksichtigten Variablen erstellt werden. Hier kann es drei verschiedene Interpretationsmöglichkeiten geben:
- Variable A beeinflusst Variable B
- Variable B beeinflusst Variable A
- Der Faktor C (gemeinsame Hintergrundvariable) beeinflusst Variable A und B
Da bei der Faktorenanalyse immer mit Möglichkeit 3 gearbeitet wird, bedeutet dies im Umkehrschluss: Eine Faktorenanalyse ist nur dann möglich, wenn die dritte Option sachlogisch ist.
Die Korrelationsmatrix zeigt zudem auf, welche Variablen für die Faktorenanalyse berücksichtigt werden sollten – jene, die kaum Berührungspunkte zu den anderen haben, können ausgeschlossen werden.
Faktorenextraktion: Grundannahmen
Nun müssen die vorhandenen Variablen auf Hintergrundvariablen aufgeteilt, also die Faktoren extrahiert werden. Dabei gelten die folgenden Bedingungen:
- Jeder Wert einer Ausgangsvariablen lässt sich als Linearkombination hypothetischer Faktoren beschreiben.
- Der Begriff „Faktorladung“ bezieht sich auf die Stärke des Zusammenhangs zwischen dem Faktor und der Variablen.
- Der Zusammenhang zwischen den Variablen ist mathematisch formulierbar:
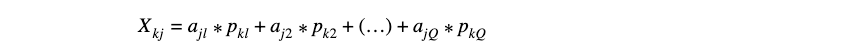
- Die mathematische Formel mit den standardisierten Werten sieht dann wie folgt aus:
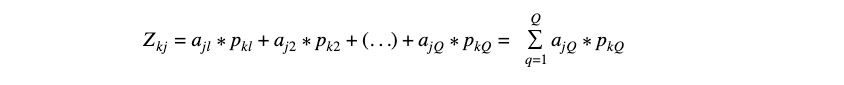
- Also vereinfacht: Z=P+A‘
- Daraus wird das Fundamentaltheorem von Thurstone hergeleitet: R=A*C*A‘
- R ist die Korrelationsmatrix; A ist die Faktorladung; C ist die Korrelation zwischen den Faktoren.
- Die mathematische Formel mit den standardisierten Werten sieht dann wie folgt aus:
- Sind die Faktoren voneinander unabhängig und ist eine Linearverknüpfung vorhanden, dann gilt das gekürzte Fundamentaltheorem: R=A*A‘
Nun lässt sich die Faktorenextraktion grafisch in einem Vektor-Diagramm darstellen.
Faktorenextraktion: Kommunalitäten definieren
Je weniger Faktoren extrahiert werden, desto mehr Informationen gehen verloren. Diese als Varianz bezeichnete Abweichung lässt sich auch auf Ebene einzelner Variablen berechnen. Der Wert, der dabei herauskommt, wird Kommunalität genannt – er gibt an, wieviel der Varianz einer Variablen durch die Faktoren erklärt werden kann. Die Kommunalität wird als Unbekannten-Komponente U der obigen Formel hinzugefügt. Um diesen Schätzwert zu bestimmen gibt es zwei Optionen:
- Es wird angenommen, dass die Faktoren die gesamte Varianz erklären können. Daher ist die Summe der Kommunalitäten immer 1.
- Ein Schätzwert wird aufgrund von Überlegungen vorgegeben. Dies ist meist der höchste quadrierte Korrelationseffizient der Korrelationsmatrix R.
Durchführung der Faktorenextraktion: Methoden
Zur Durchführung einer Faktorenextraktion bestehen zwei Möglichkeiten, eine Hauptachsen- oder eine Hauptkomponentenanalyse:
- Hauptachsenanalyse: Hier gilt die Annahme, dass die Varianz einer Ausgangsvariablen immer auf Einzelrestvarianz und Kommunalitäten aufgeteilt ist. Die Höhe der Kommunalitäten muss daher geschätzt werden. Dabei sollen die Faktoren die Varianzen der Variablen in der Höhe der Kommunalitäten erklären.
- Hauptkomponentenanalyse: Es wird angenommen, dass die Varianz einer Ausgangsvariablen komplett durch die Faktorenextraktion erklärt werden kann. Das Ziel ist, mit möglichst wenigen Faktoren die Datenstruktur möglichst umfassend zu reproduzieren. Daher gibt es hier keine Unterscheidung zwischen Kommunalitäten und Einzelrestvarianzen.
Festlegen der Faktorenanzahl
Es gibt weder die richtige Anzahl an Faktoren noch allgemeingültige Richtlinien zu ihrer Bestimmung. Um die Entscheidung zu vereinfachen, helfen allerdings verschiedene Kriterien:
- Es wird so lange extrahiert, bis eine festgelegte Prozentzahl der Varianz erklärt ist. Varianz bezeichnet in diesem Fall die Standardabweichung.
- Kaiser-Kriterium: Alle Faktoren, die einen Eigenwert von über eins haben, werden extrahiert. Eigenwert bedeutet die Summe aller quadrierten Faktorladungen eines Faktors über alle Variablen.
- Scree-Test oder auch Ellenbogenkriterium: Die Eigenwerte der Faktoren werden im Screeplot (Eigenwertdiagramm) abnehmend eingeordnet.
- Vorab wird inhaltlich eine bestimmte Anzahl an Faktoren festgelegt.
- Die Zahl der Faktoren soll geringer sein als die Hälfte der Variablen.
- Alle Faktoren, die interpretiert werden können, werden extrahiert.
Interpretation der Faktorenanalyse
Da die Faktoren, die im vorangegangenen Schritt extrahiert wurden, nur schwer auszuwerten sind, werden sie nun transformiert. Dies wird als Rotation bezeichnet.
Zunächst erfolgt allerdings eine Analyse der (unrotierten) Faktorladungen. Dabei muss der Analysierende eine umfassende Kenntnis der inhaltlichen Thematik haben. Wurde vorher eine Hauptachsenanalyse vorgenommen, erfolgt die Interpretation nun kausal. Ist stattdessen eine Hauptkomponentenanalyse durchgeführt worden, ist das nicht möglich und auch nicht nötig. Denn in diesem Fall gibt es keine Faktorenrotation.
Faktorrotation zur einfacheren Analyse der Faktoren
Vor der Rotation können die den Faktoren zugewiesenen Variablen unterschiedlich stark mit ihnen korrelieren – sie haben also verschiedene Faktorladungen. Dies macht die Interpretation schwieriger, da die Gewichtung eines Faktors nicht vollends geklärt ist. Aus diesem Grund werden die Faktorladungen rotiert, wie in dieser Grafik ersichtlich wird:
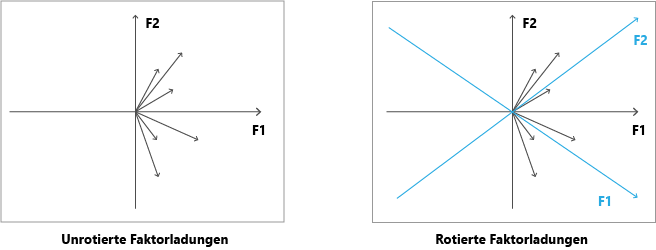
Dabei werden die Koordinationsachsen des Diagramms in ihrem Ursprung rotiert, sodass sich die Faktorladungen sinnvoller auf die Faktoren aufteilen. Denn sowohl die Faktorenladungen als auch die Eigenwerte verändern sich, während die Kommunalitäten gleich bleiben.
Zur Auswahl stehen zwei verschiedene Rotationsverfahren:
- Orthogonale (rechtwinklige) Rotation: Hier besteht die Annahme, dass Faktoren untereinander nicht korrelieren. Aus diesem Grund stehen ihre Vektoren immer senkrecht zueinander. Unterdessen bleiben die Faktorenachsen während der Rotation einander stets im rechten Winkel ausgerichtet.
- Oblique (schiefwinklige) Rotation: Bei dieser Rotation wird dagegen angenommen, dass die Faktoren untereinander korrelieren. Daher können sich die Winkel zwischen den Faktoren während des Rotationsvorganges verschieben. Der Vorteil ist, dass die Faktorladungen sehr viel genauer auf die Faktoren aufgeteilt werden. Gleichzeitig widerspricht dieses Modell einer der Grundannahmen der Faktorenanalyse: Die Faktoren sind hier nicht mehr unabhängig voneinander.
Faktorenwerte interpretieren
Als letzter Schritt der Faktorenanalyse erfolgt nun die Interpretation der Faktorenwerte. Diese können sowohl positiv oder negativ ausfallen oder nahe der Null liegen. Die Faktorenwerte können folgendermaßen interpretiert werden:
- Positive Werte: Das Objekt ist hinsichtlich des betrachteten Faktors sowie im Vergleich zu anderen Objekten überdurchschnittlich ausgeprägt.
- Negative Werte: Das Objekt ist hinsichtlich des betrachteten Faktors sowie im Vergleich zu anderen Objekten unterdurchschnittlich ausgeprägt.
- Faktorwert liegt nahe Null: Das Objekt ist hinsichtlich des betrachteten Faktors sowie im Vergleich zu anderen Objekten durchschnittlich ausgeprägt.
Mehr über Qualtrics
Demo anfordernFaktorenanalyse: Beispiel
In diesem Beispiel einer Faktorenanalyse möchte ein Hersteller von Eistee seine Produkte im Wettbewerbsumfeld ideal positionieren. Daher sollen Veränderungen am Produkt über einen längeren Zeitraum beobachtet und deren Auswirkungen auf die Zielgruppen gemessen werden.
Um das Messinstrument optimal zu entwickeln, definiert das Unternehmen im ersten Schritt Variablen, um eine qualitative Studie durchführen zu können. Zunächst soll getestet werden, ob diese Variablen hinsichtlich des Untersuchungsziels valide sind.
In diesem Rahmen sollen folgende Fragestellungen beantwortet werden:
- Ist es möglich, auf Basis der Variablen wesentliche Bewertungsdimensionen abzuleiten, die eine komprimierte Ergebnisdarstellung zulassen?
- Können die Variablen ausreichend präzise definiert werden, um den jeweiligen Dimensionen eindeutig zugeordnet werden zu können?
- Gibt es in der Liste redundante Merkmale, deren Streichung den Aufwand der Studie erheblich verringern würde?
- Sind die Merkmale inhaltlich valide? Liefern sie die gesuchte Information?
Variablen, die untersucht werden
Innerhalb der beispielhaften Faktorenanalyse werden folgende Variablen untersucht:
| V01 | Schmeckt nach Tee |
| V02 | Angenehmer Geschmack |
| V03 | Intensiver Geschmack |
| V04 | Bitter |
| V05 | Süß |
| V06 | Konzentrationsfördernd |
| V07 | Übler Geruch |
| V08 | Gut verträglich |
| V09 | Erfrischend |
| V10 | Durstlöschend |
| V11 | Mild |
| V12 | Verdauungsfördernd |
| V13 | Allergikerfreundlich |
| V14 | Unbekömmlich |
| V15 | Anregend |
| V16 | Künstlicher Geschmack |
Die nachfolgende Bewertung erfolgt auf einer Skala mit sieben Stufen. Dabei trifft 1 überhaupt nicht zu und 7 trifft voll und ganz zu.
Beispiel einer Hauptkomponentenanalyse
Mithilfe der Hauptkomponentenanalyse werden die Merkmale Schritt für Schritt extrahiert. Zusätzlich nehmen sie einen maximalen Teil der Varianz auf.
In dieser Abbildung sind die Eigenwerte der Hauptkomponenten ersichtlich, dies entspricht bei der Hauptkomponentenanalyse der Varianz. Die Varianz nimmt von Komponente 1 bis zu Nummer 16 immer weiter ab. Insgesamt ergibt die kumulierte Summe der Eigenwerte 100 Prozent.
| Komponente | Gesamt | % der Varianz | Kumulierte % |
|---|---|---|---|
| 1 | 6,462 | 40,386 | 40,386 |
| 2 | 2,773 | 17,330 | 57,716 |
| 3 | 1,525 | 9,530 | 67,246 |
| 4 | 0,869 | 5,432 | 72,678 |
| 5 | 0,713 | 4,454 | 77,132 |
| 6 | 0,643 | 4,018 | 81,150 |
| 7 | 0,496 | 3,101 | 84,251 |
| 8 | 0,475 | 2,968 | 87,219 |
| 9 | 0,415 | 2,591 | 89,810 |
| 10 | 0,364 | 2,275 | 92,085 |
| 11 | 0,319 | 1,992 | 94,077 |
| 12 | 0,256 | 1,601 | 95,678 |
| 13 | 0,217 | 1,357 | 97,035 |
| 14 | 0,184 | 1,148 | 98,183 |
| 15 | 0,165 | 1,029 | 99,212 |
| 16 | 0,126 | 0,788 | 100,000 |
Beispiel für das Festlegen der Faktorenanzahl
Für das Festlegen der Faktorenanzahl wird in diesem Beispiel der Scree-Test herangezogen:
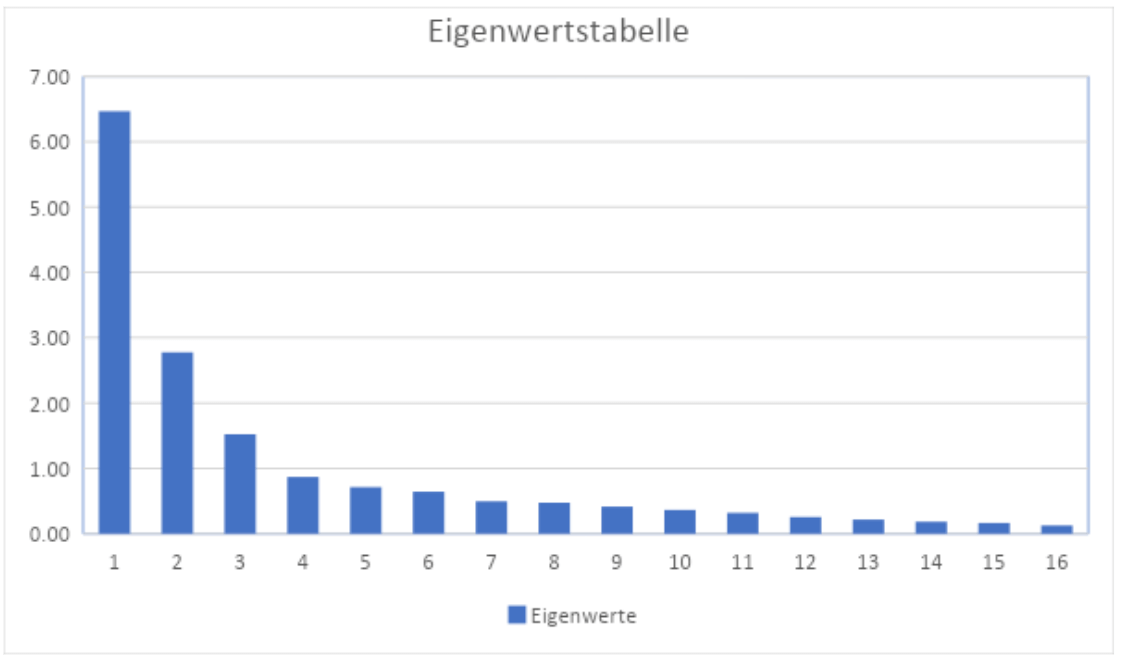
Bei dieser als Ellbogendiagramm bezeichneten Grafik zeigt die „Beuge“ an, welche Anzahl von Faktoren am besten geeignet ist. Da die Beuge in diesem Fall auf der senkrechten Achse etwa bei 3 beginnt, sollten hier drei Dimensionen extrahiert werden.
Interpretation der Beispiel-Faktorenanalyse
Innerhalb der Faktoranalyse werden die Variablen in drei Dimensionen / Faktoren eingeteilt. Unter Berücksichtigung der Korrelationsmatrix ergibt sich nach der Faktorenanalyse folgende Interpretation:
| Faktor 1 | Faktor 2 | Faktor 3 |
|---|---|---|
| V01 Schmeckt nach Tee | V08 Gut verträglich | V04 Bitter |
| V02: Angenehmer Geschmack | V11 Mild | V07 Übler Geruch |
| V03 Intensiver Geschmack | V12 Verdauungsfördernd | V14 Unbekömmlich |
| V10 Durstlöschend | V13 Allergikerfreundlich | V16 Künstlicher Geschmack |
| V05 Süß | ||
| V06 Konzentrationsfördernd | ||
| V09 Erfrischend | ||
| V15 Anregend |
- Faktor 1 enthält Variablen, die sich auf den Geschmack und die Wirkung beziehen. Hier korrespondieren also gleich zwei Dimensionen von Variablen.
- Faktor 2 beinhaltet Variablen, die sich auf die Verträglichkeit des Produkts beziehen.
- Faktor 3 fasst Merkmale zusammen, die störend wirken, also als Störreize bezeichnet werden können.
Wann sich eine Faktoranalyse eignet
Eine große Herausforderung der Statistik ist das Erfassen von latenten Variablen. Diese sind im Gegensatz zu manifesten Variablen nicht direkt messbar. Daher werden Verfahren benötigt, um mit diesen Variablen arbeiten zu können. Die Faktorenanalyse ist eines davon. Sie unterstützt nicht nur dabei, diese latenten Variablen herauszufiltern, sondern ihren Informationsgehalt möglichst relevant auf einzelne Faktoren aufzuteilen.
So können beispielsweise Umfragen, Marktforschungen und Fragebögen viel unkomplizierter ausgewertet werden.
Bereit anzufangen? Fordern Sie jetzt Ihre Demoversion an!