Interprétation des tracés résiduels pour améliorer votre régression
Lorsque vous exécutez une régression, Stats iQ calcule et trace automatiquement les résiduels pour vous aider à comprendre et à améliorer votre modèle de régression. Cet article contient tout ce que vous devez savoir sur l’interprétation des résiduels (y compris des définitions et des exemples).
Observations, prédictions et résiduels
Pour montrer comment interpréter les résiduels, nous utiliserons un ensemble de données de stands de limonade, où chaque ligne correspondait à un jour de « Température » et de « Chiffre d’affaires ».
| Température (Celsius) | Chiffre d’affaires |
|---|---|
| 28,2 | 44 USD |
| 21,4 | 23 USD |
| 32,9 | 43 USD |
| 24,0 | 30 USD |
| etc. | etc. |
L’équation de régression décrivant la relation entre la « Température » et le « Chiffre d’affaires » est la suivante :
Chiffre d’affaires = 2,7 * Température – 35
Disons qu’un jour, il faisait 30,7 degrés au stand de limonade et que le « Chiffre d’affaires » était de 50 $. Ce chiffre 50 est votre variable de sortie observée ou réelle, la valeur qui s’est réellement produite.
Donc, si nous insérons 30,7 à notre valeur pour la « Température »…
Chiffre d’affaires = 2,7 * 30,7 – 35
Chiffre d’affaires = 48
…nous obtenons 48 $. Il s’agit de la valeur prédite pour ce jour, également appelée valeur du « Chiffre d’affaires » que l’équation de régression aurait estimée en fonction de la « Température ».
Votre modèle n’est pas toujours parfait, bien sûr. Dans ce cas, la prédiction a un écart de 2 ; cette différence, le 2, est appelée le résiduel. Le résiduel est ce qui reste lorsque vous soustrayez la valeur prédite de la valeur observée.
Résiduel = Observé – Prédit
Vous pouvez imaginer que chaque ligne de données possède désormais, en plus, une valeur prédite et une valeur résiduelle.
| Température (Celsius) |
Chiffre d’affaires (Observé) |
Chiffre d’affaires (Prédit) |
Résiduel (Observé – Prédit) |
|---|---|---|---|
| 28,2 | 44 USD | 41 USD | 3 USD |
| 21,4 | 23 USD | 23 USD | 0 USD |
| 32,9 | 43 USD | 54 USD | -11 USD |
| 24,0 | 30 USD | 29 USD | 1 USD |
| etc. | etc. | etc. | etc. |
Nous allons utiliser les valeurs observées, prédites et résiduelles pour évaluer et améliorer le modèle.
Comprendre la précision à l’aide de la fonction Observé et Prédit
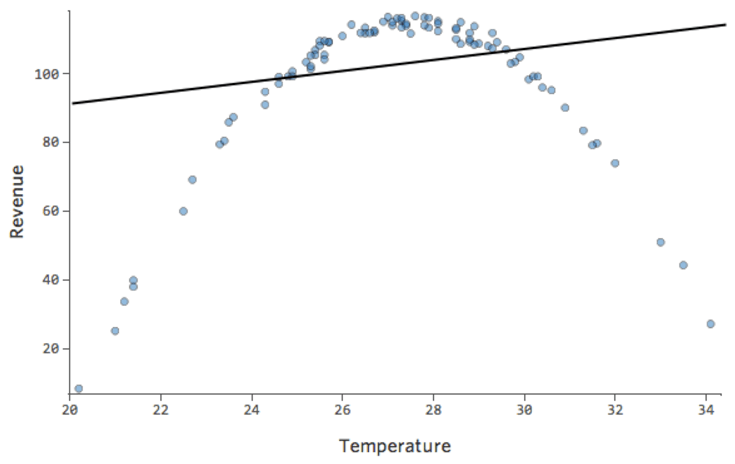
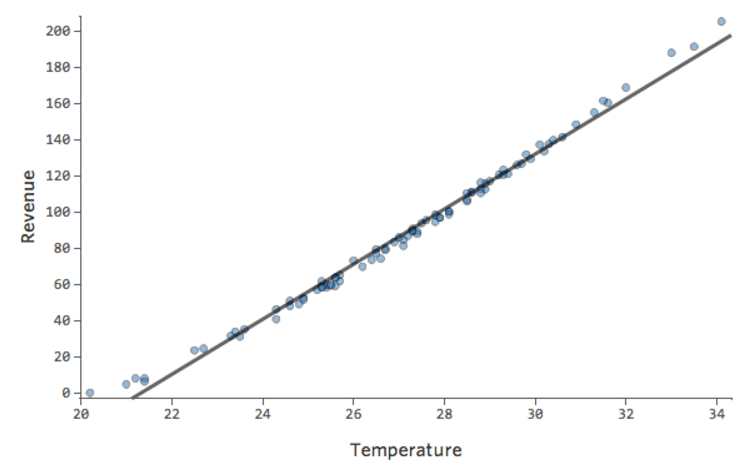
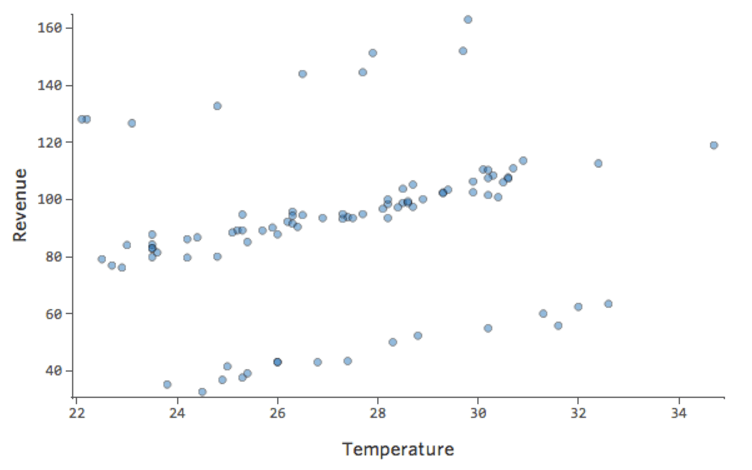
Dans un modèle simple comme celui-ci, avec seulement deux variables, vous pouvez avoir une idée de la précision du modèle en associant « Température » et « Chiffre d’affaires ». Voici la même analyse de régression effectuée sur deux stands de limonade différents, l’un où le modèle est très précis, l’autre où le modèle ne l’est pas :
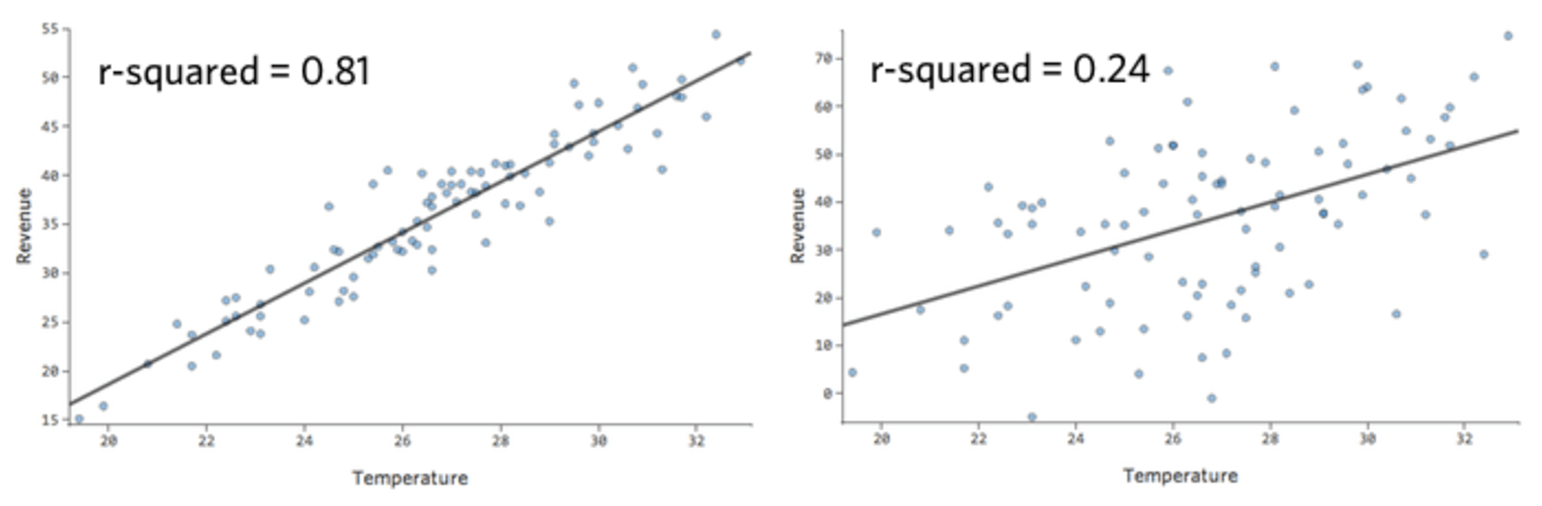
Il est clair que pour les deux stands de limonade, une « Température » plus élevée est associée à un « Chiffre d’affaires » plus élevé. Cependant, à une « Température » donnée, vous pouvez estimer le « Chiffre d’affaires » du stand de limonade de gauche avec beaucoup plus de précision que pour celui de droite, ce qui signifie que le modèle est beaucoup plus précis.
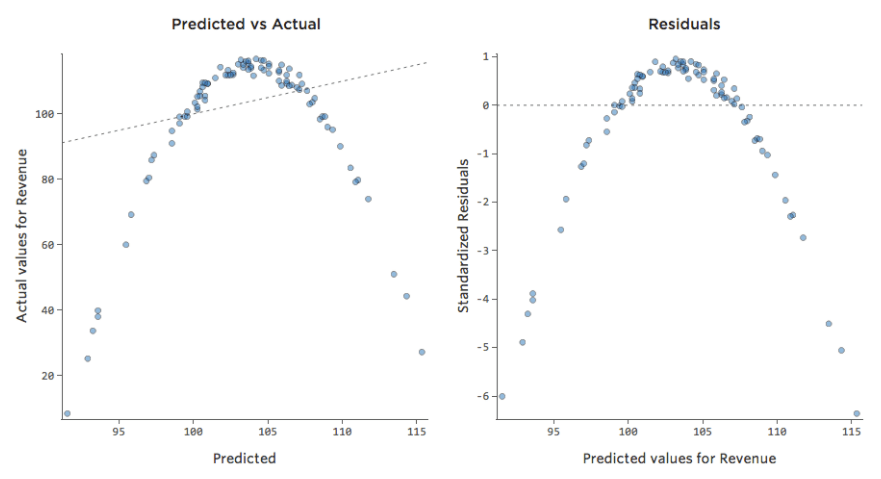
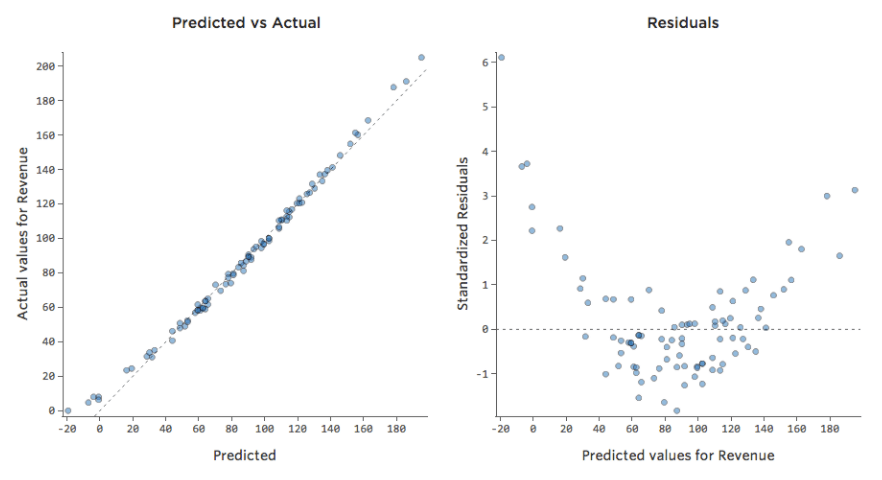
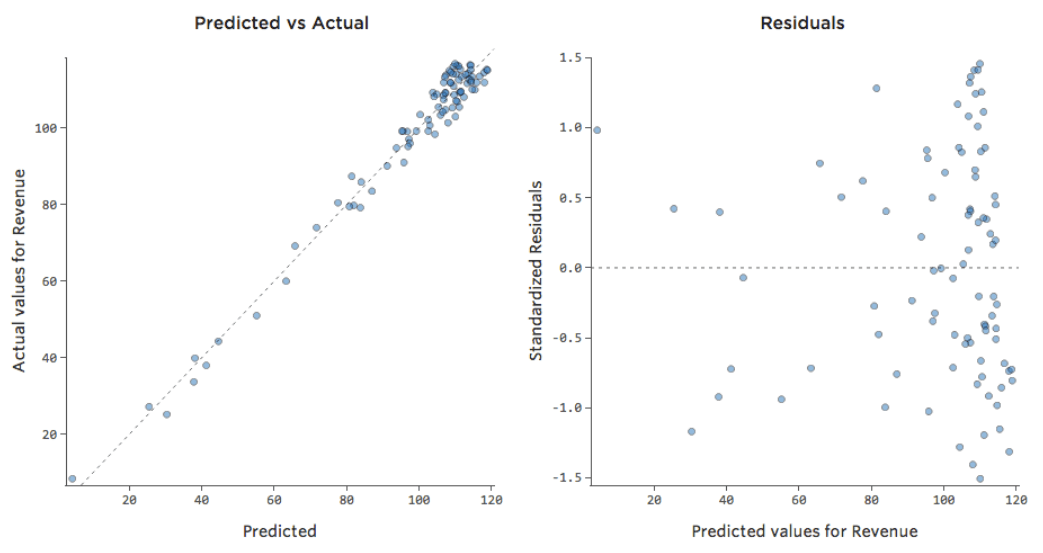
La plupart des modèles ont plus d’une variable explicative et il n’est pas pratique de représenter plus de variables dans un graphique comme celui-ci. À la place, traçons les valeurs prédites par rapport aux valeurs observées pour ces mêmes ensembles de données.
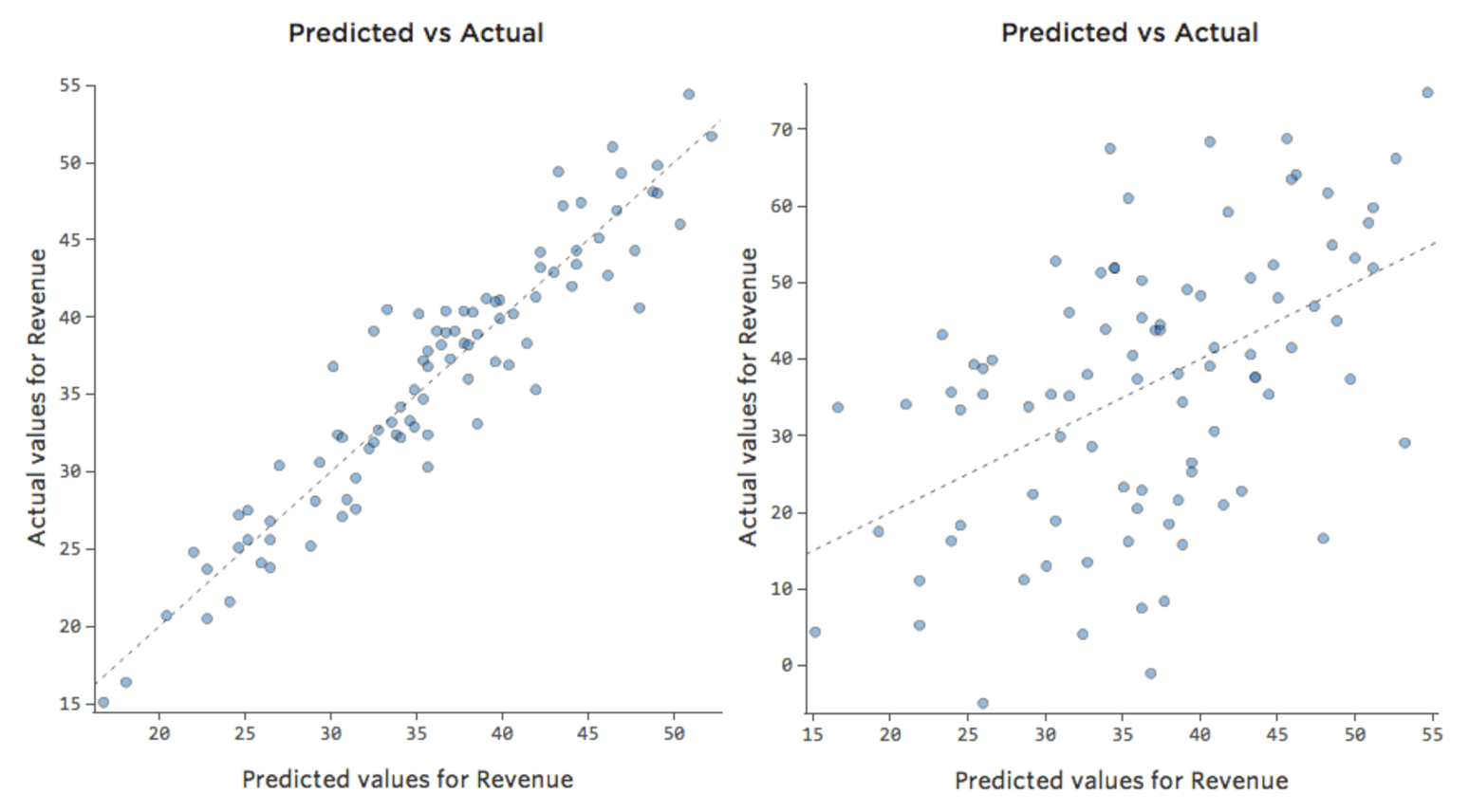
Encore une fois, le modèle du graphique de gauche est très précis ; il existe une forte corrélation entre les prédictions du modèle et ses résultats réels. Avec le modèle pour le graphique de droite, c’est le contraire ; les prédictions du modèle ne sont pas très bonnes.
Notez que ces graphiques ressemblent aux graphiques « Température » par rapport au « Chiffre d’affaires » au-dessus d’eux, mais l’axe des x est prédit « Chiffre d’affaires » au lieu de « Température. » C’est courant lorsque votre équation de régression n’a qu’une seule variable explicative. Mais plus souvent, vous aurez plusieurs variables explicatives, et ces graphiques auront un aspect assez différent d’un graphique représentant n’importe quelle variable explicative vs. “Chiffre d’affaires”.
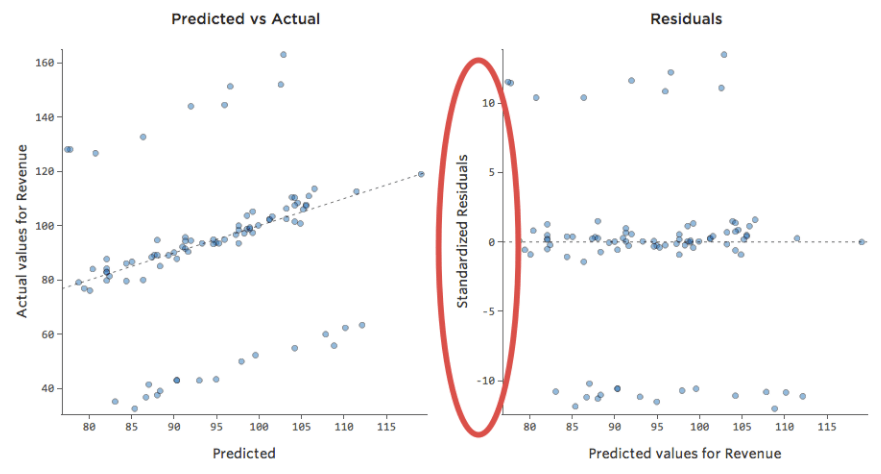
Examen Prédit vs. Résiduel (« Le tracé résiduel »)
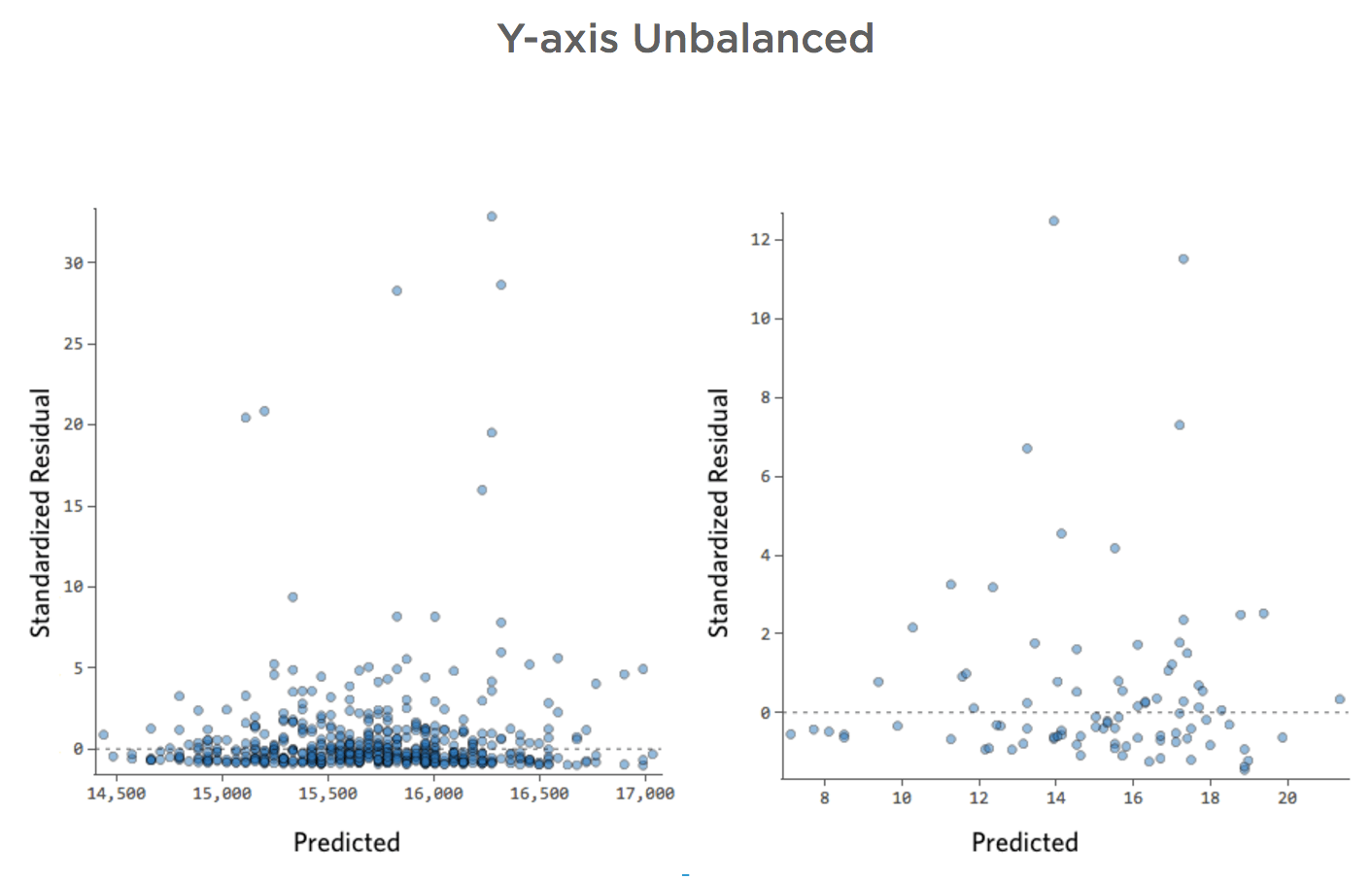
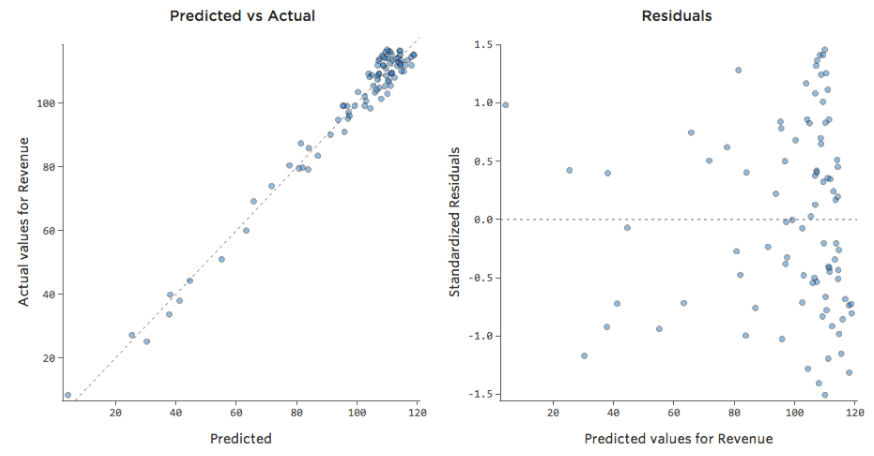
La manière la plus utile de tracer les résiduels, cependant, est avec vos valeurs prédites sur l’axe des abscisses et vos résiduels sur l’axe des ordonnées.
(Stats iQ présente les résiduels sous forme de résiduels standardisés, ce qui signifie que chaque tracé résiduel que vous examinez avec n’importe quel modèle se trouve sur le même axe des ordonnées standardisé.)
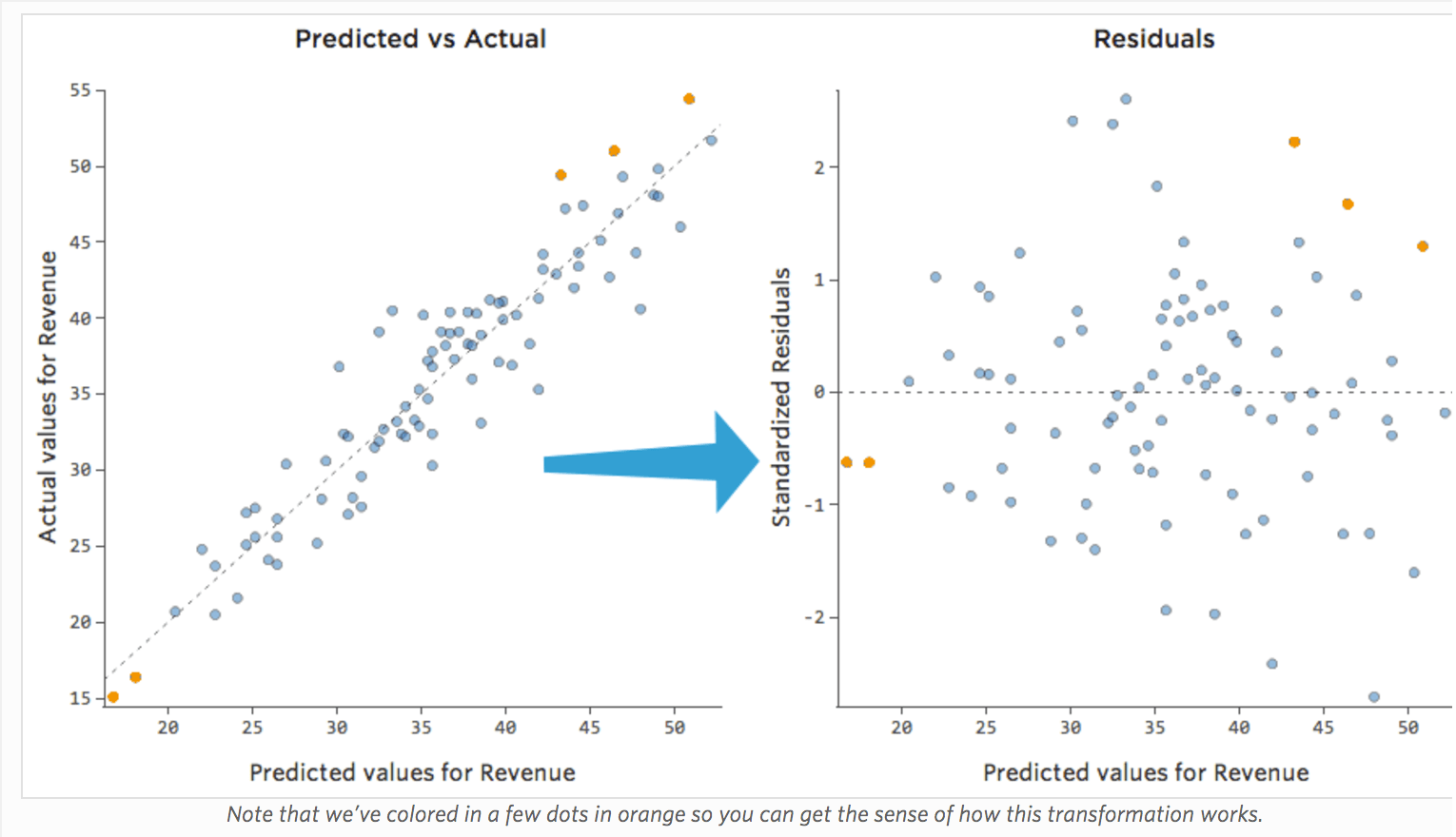
Dans le tracé de droite, chaque point représente un jour, où la prédiction faite par le modèle est sur l’axe des abscisses et la précision de la prédiction est sur l’axe des ordonnées. La distance de la ligne jusqu’au 0 correspond à l’imprécision de la prédiction de cette valeur.
Puisque…
Résiduel = Observé – Prédit
…Les valeurs positives pour la valeur résiduelle (sur l’axe des ordonnées) signifient que la prédiction était trop faible, et les valeurs négatives signifient que la prédiction était trop élevée ; 0 signifie que la supposition était exacte.
Dans l’idéal, votre tracé des valeurs résiduelles ressemble à l’un de ceux-ci :
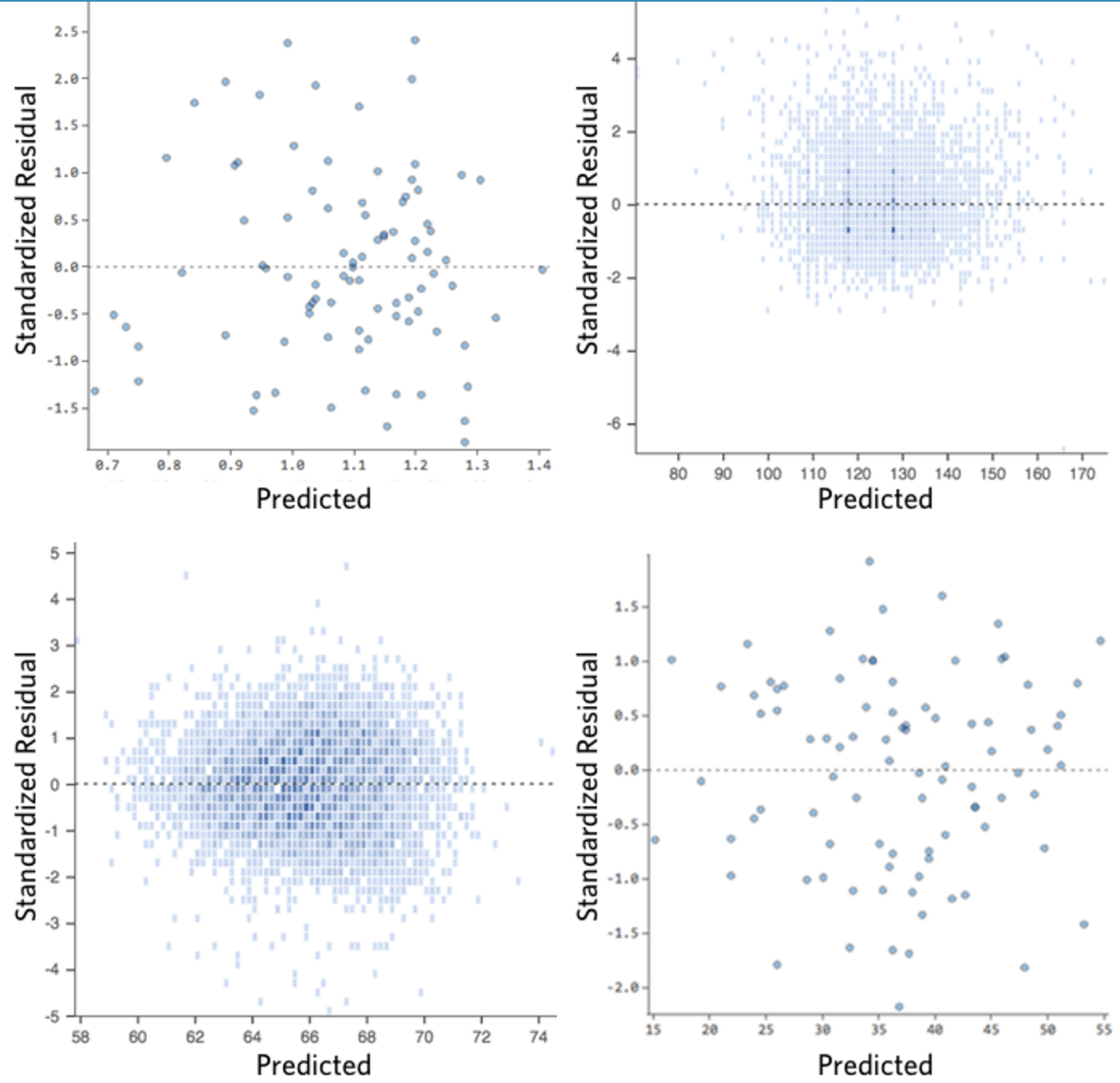
C’est-à-dire :
(1) ils sont assez symétriquement distribués, tendant à se regrouper vers le milieu du tracé.
(2) ils sont regroupés autour des nombres à un chiffre les plus bas de l’axe des ordonnées (par exemple, 0,5 ou 1,5, et non 30 ou 150).
(3) en général, il n’y a pas de tendances nettes.
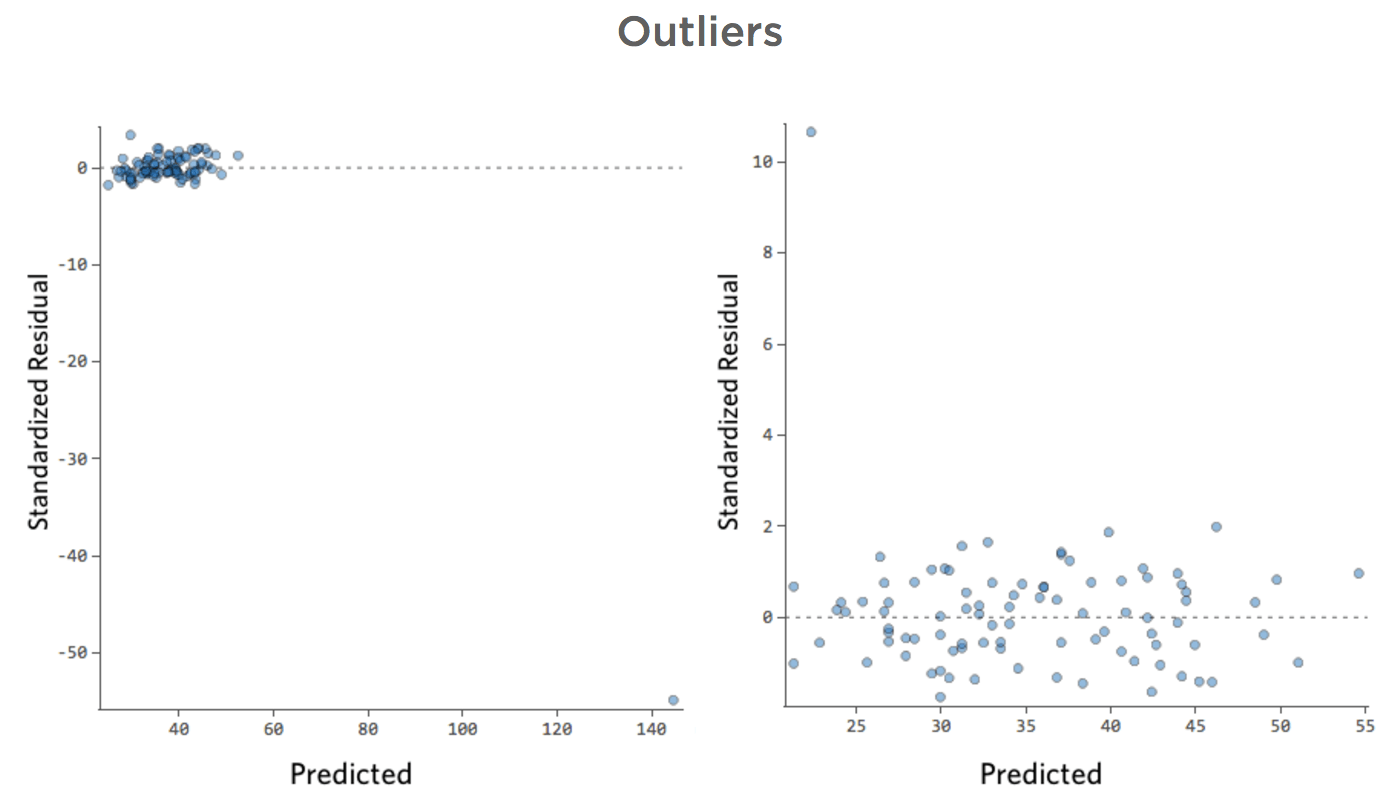
Voici quelques tracés résiduels qui ne répondent pas à ces conditions :
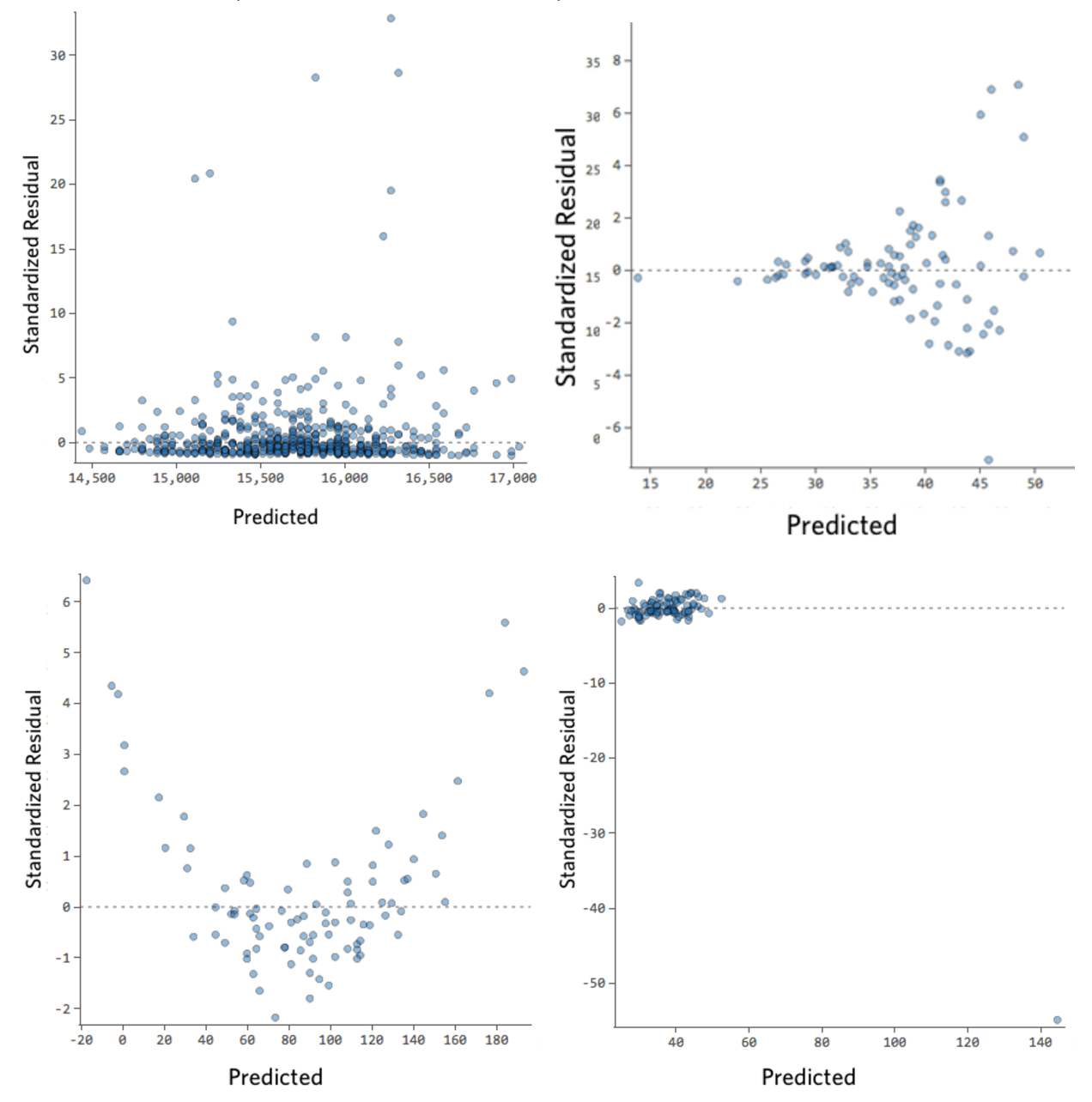
Ces tracés ne sont pas distribués verticalement uniformément, ou ils ont une valeur aberrante, ou ils montrent un motif ou une tendance claire.
Si vous pouvez détecter un motif ou une tendance claire dans vos résiduels, votre modèle dispose alors d’une marge d’amélioration.
Nous allons ensuite expliquer pourquoi cela arrive et que faire pour améliorer votre modèle.
Tracé résiduel Q-Q normal :
Cliquez sur Afficher le tracé résiduel Q-Q normal pour afficher un tracé Q-Q évaluant l’asymétrie des données et l’adaptation du modèle. Ce diagramme affiche les résiduels standardisés sur l’axe y et les quantiles théoriques sur l’axe x.
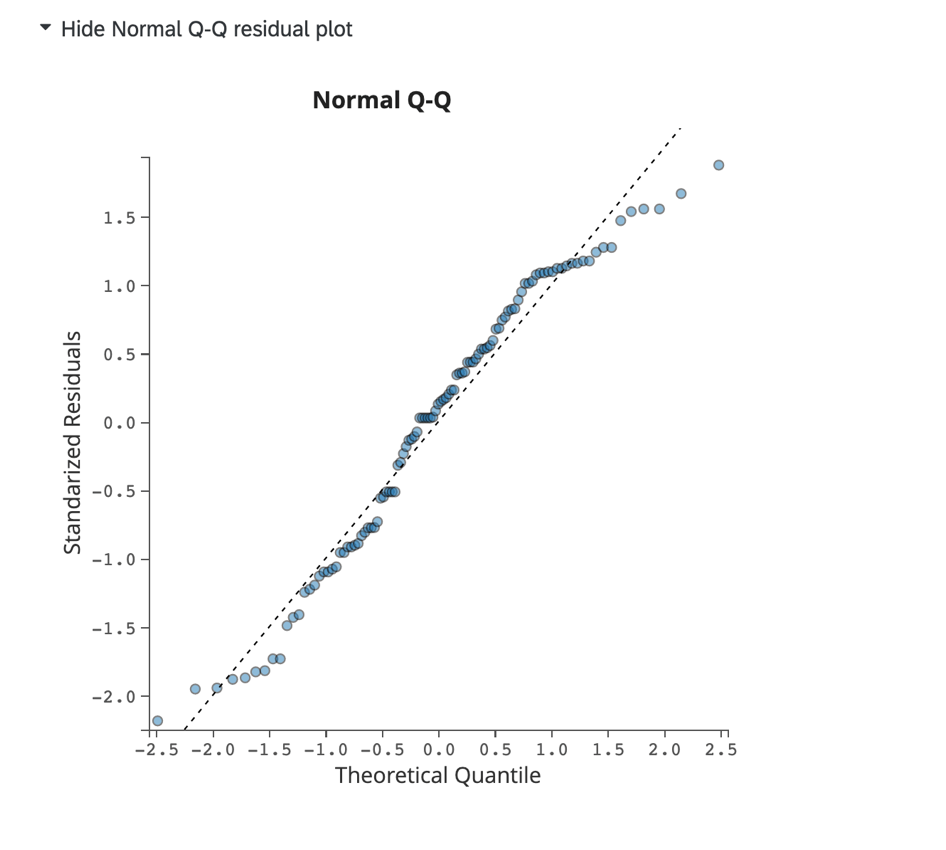 Les données qui s’alignent étroitement sur la ligne pointillée indiquent une distribution normale. Si les points s’écartent drastiquement de la ligne, vous pouvez envisager d’ajuster votre modèle en ajoutant ou en supprimant d’autres variables dans le modèle de régression.
Les données qui s’alignent étroitement sur la ligne pointillée indiquent une distribution normale. Si les points s’écartent drastiquement de la ligne, vous pouvez envisager d’ajuster votre modèle en ajoutant ou en supprimant d’autres variables dans le modèle de régression.
Est-ce important si mon modèle n’est pas parfait ?
Dans quelle mesure devriez-vous vous inquiéter si votre modèle n’est pas parfait, si vos résiduels ont l’air un peu mauvais ? C’est à vous de voir.
Si vous publiez votre thèse en physique des particules, vous voudrez probablement vous assurer que votre modèle est aussi précis que possible. Si vous essayez d’effectuer une analyse « vite fait bien fait » du stand de limonade de votre neveu, un modèle imparfait pourrait suffire à répondre à toutes les questions que vous vous posez (p. ex., si la « Température » semble affecter le « Chiffre d’affaires »).
La plupart du temps, mieux vaut un modèle décent qu’aucun modèle. Alors, prenez votre modèle, essayez de l’améliorer, puis décidez si la précision est suffisamment bonne en fonction de vos besoins.
Exemple de tracés résiduels et leurs diagnostics
Si vous n’êtes pas sûr de ce qu’est un résiduel, prenez cinq minutes pour lire ce qui précède, puis revenez ici.
Vous trouverez ci-dessous une galerie de tracés résiduels mauvais. Votre tracé résiduel peut ressembler à un type spécifique ci-dessous, ou à une combinaison.
S’il ressemble à l’un de ceux présentés ci-dessous, cliquez dessus pour comprendre ce qui se passe et comment corriger le problème.
(Nous utiliserons le « Chiffre d’affaires » d’un stand de limonade par rapport à la « Température » de ce jour-là comme exemple d’ensemble de données.)
Axe des ordonnées déséquilibré
- Afficher les détails sur ce tracé et comment le corriger.
-
Problème
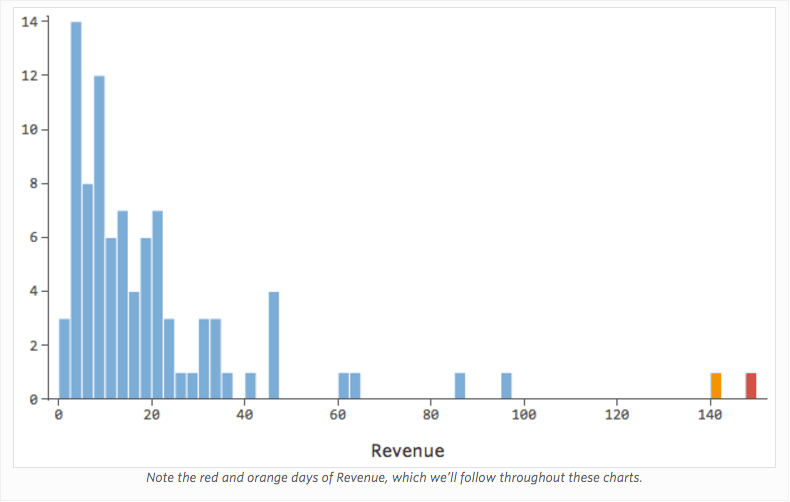
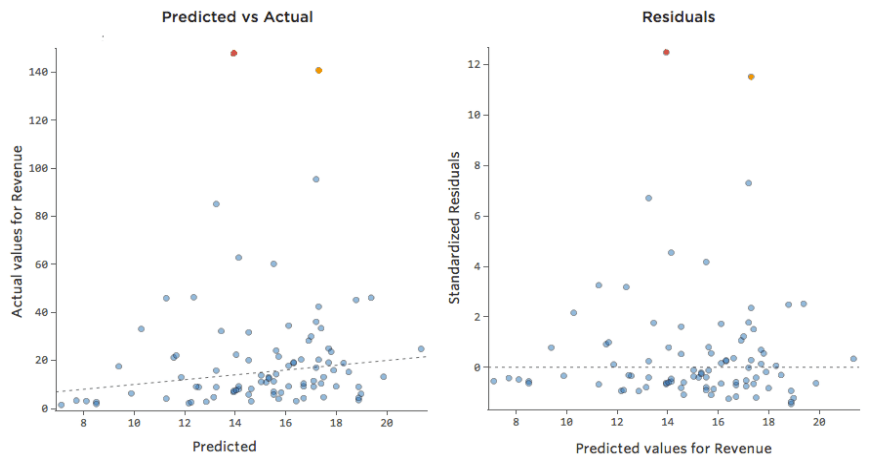
Imaginez que, pour une raison quelconque, votre stand de limonade a généralement un chiffre d’affaires bas, mais que de temps en temps vous avez des jours avec un chiffre d’affaires très élevé, de sorte que le « Chiffre d’affaires » ressemble à cela…
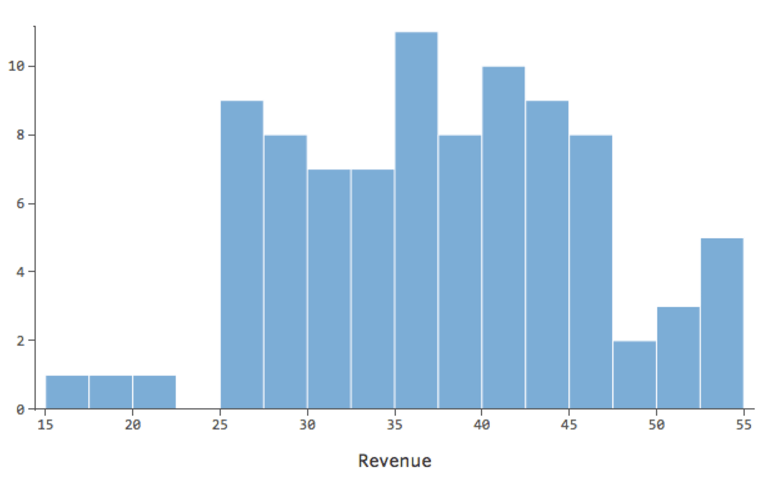
…au lieu d’obtenir que quelque chose de plus symétrique et en forme de cloche comme ceci :
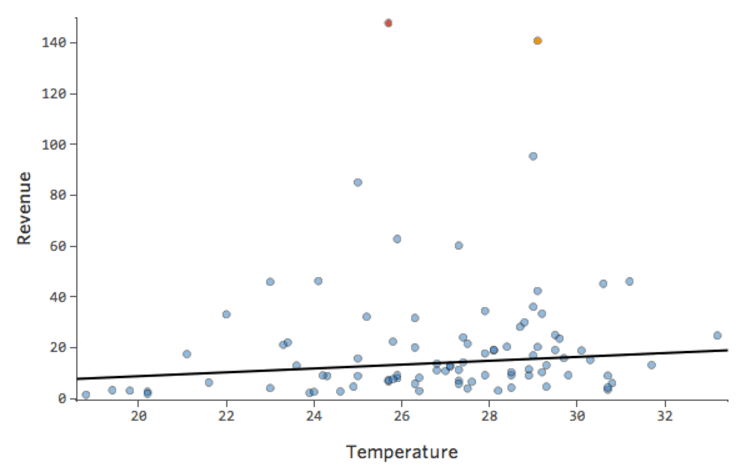
Donc « Température » vs. « chiffre d’affaires » pourrait ressembler à cela, la plupart des données étant regroupées en bas…
La ligne noire représente l’équation du modèle, la prédiction du modèle de la relation entre « Température » et « Chiffre d’affaires ». Regardez au-dessus de chaque prédiction faite par la ligne noire pour une « Température » donnée (p. ex., avec une « Température » de 30, le « Chiffre d’affaires » devrait être d’environ 20). Vous pouvez voir que la majorité des points sont sous la ligne (c’est-à-dire que la prédiction était trop élevée), mais quelques points sont très loin au-dessus de la ligne (c’est-à-dire que la prédiction était beaucoup trop faible).
En traduisant ces mêmes données dans les tracés de diagnostic, la plupart des prédictions de l’équation sont un peu trop élevées, et certaines seraient beaucoup trop faibles.
Conclusions
Cela signifie presque toujours que votre modèle peut être rendu beaucoup plus précis. La plupart du temps, vous constaterez que le modèle était correct sur le plan directionnel, mais assez inexact par rapport à une version améliorée. Il n’est pas rare de résoudre un problème comme celui-ci et, par conséquent, de voir le coefficient de détermination du modèle passer de 0,2 à 0,5 (sur une échelle de 0 à 1).
Comment corriger le modèle ?
- La solution consiste presque toujours à transformer vos données, généralement votre variable de réponse.
- Il est également possible qu’une variable manque à votre modèle.
Hétéroscédasticité
  ;
- Afficher les détails sur ce tracé et comment le corriger.
-
Problème
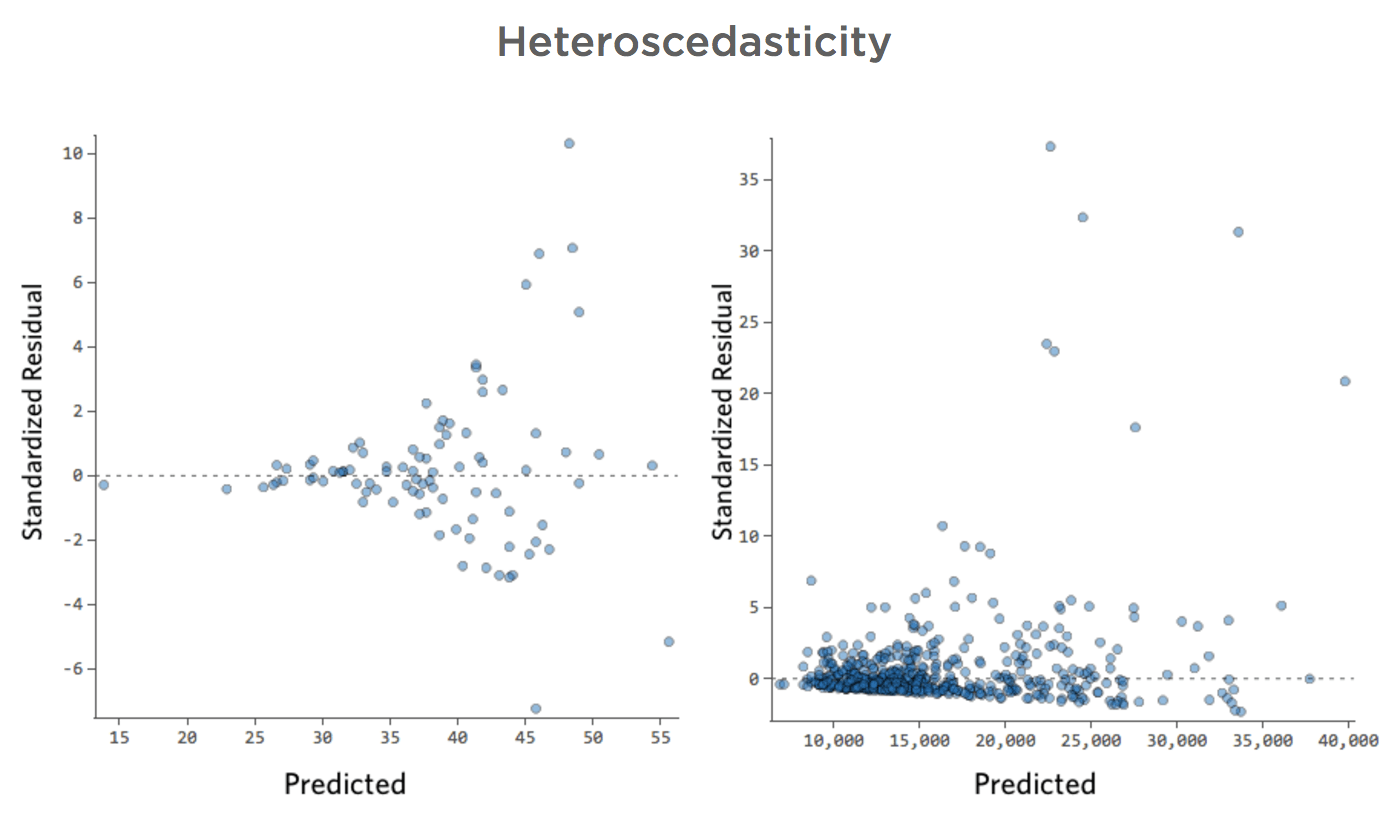
Ces tracés présentent une « hétéroscédasticité », ce qui signifie que les résiduels deviennent plus gros lorsque la prédiction passe de petite à grande (ou de grande à petite).
Imaginez que, les jours de froid, le montant du chiffre d’affaires est constant, mais les jours où il fait plus chaud, le chiffre d’affaires est parfois très élevé et parfois très faible.
Vous verriez des tracés comme ceux-ci :
Conclusions
Cela ne crée pas intrinsèquement un problème, mais cela indique souvent que votre modèle peut être amélioré.
La seule exception ici est que si la taille de votre échantillon est inférieure à 250 et que vous ne pouvez pas résoudre le problème à l’aide de l’élément ci-dessous, vos valeurs P peuvent être un peu plus élevées ou inférieures qu’elles ne devraient l’être, de sorte qu’une variable qui est juste sur la marge significative peut se retrouver par erreur du mauvais côté de cette marge. Cependant, vos coefficients de régression (le nombre d’unités dont « Revenu » change lorsque « Température » augmente de 1) seront toujours précis.
Comment corriger le modèle ?
- La solution la plus couramment retenue est de transformer une variable.
- Souvent, l’hétéroscédasticité indique qu’une variable est manquante.
Tracés non linéaires
  ;
- Afficher les détails sur ce tracé et comment le corriger.
-
Problème
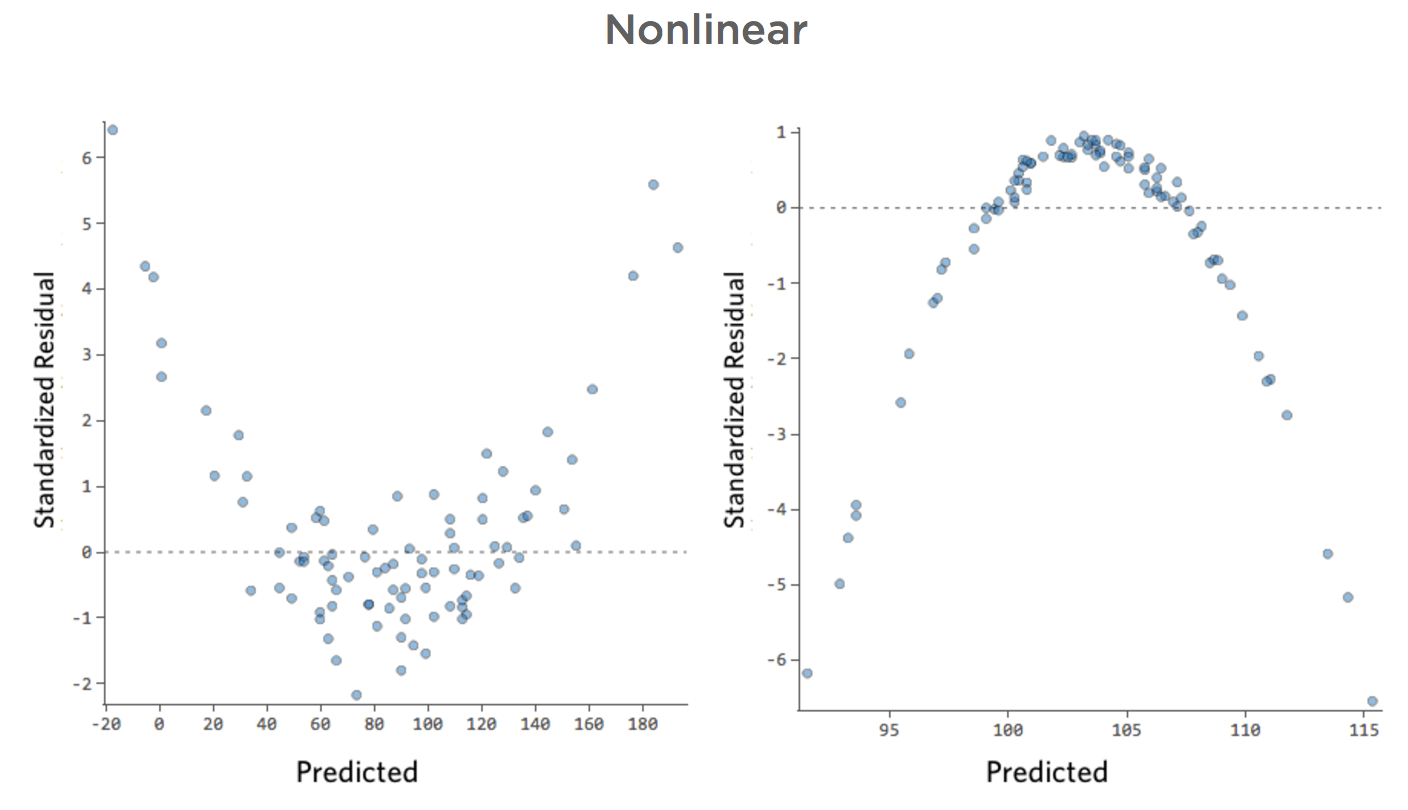
Imaginez qu’il est difficile de vendre de la limonade les jours de froid, facile de la vendre les jours où il fait chaud et difficile de la vendre les jours où il fait très chaud (peut-être parce que personne ne sort de chez soi les jours où il fait très chaud).
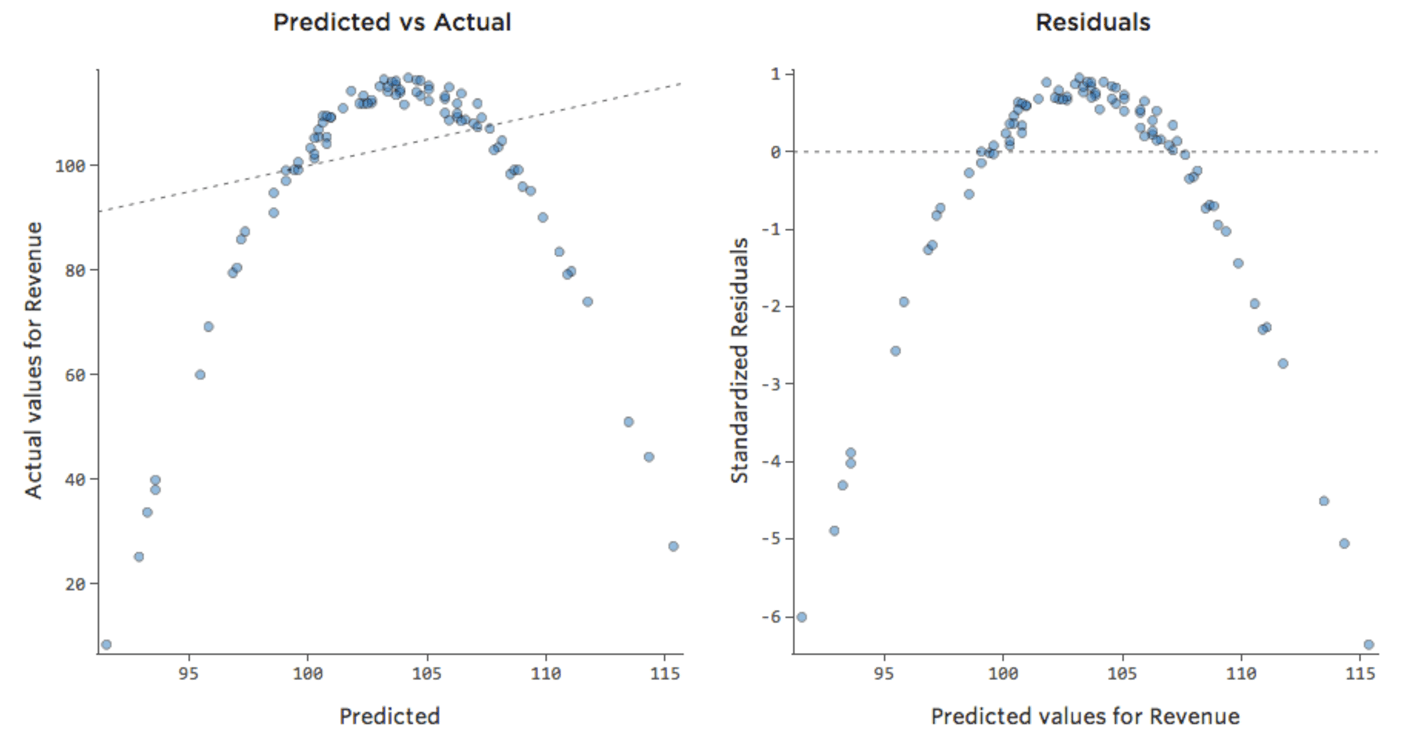
Ce tracé ressemblerait à ceci :
Le modèle, représenté par la ligne, est très mauvais. Les prédictions seraient complètement fausses, ce qui signifie que votre modèle ne représente pas avec précision le lien entre « Température » et « Chiffre d’affaires ».
En conséquence, les résiduels ressembleraient à ceci :
Conclusions
Si votre modèle est faux, comme dans l’exemple ci-dessus, vos prédictions auront peu de valeur (et vous remarquerez un coefficient de détermination très faible, p. ex. 0,027 pour le modèle ci-dessus).
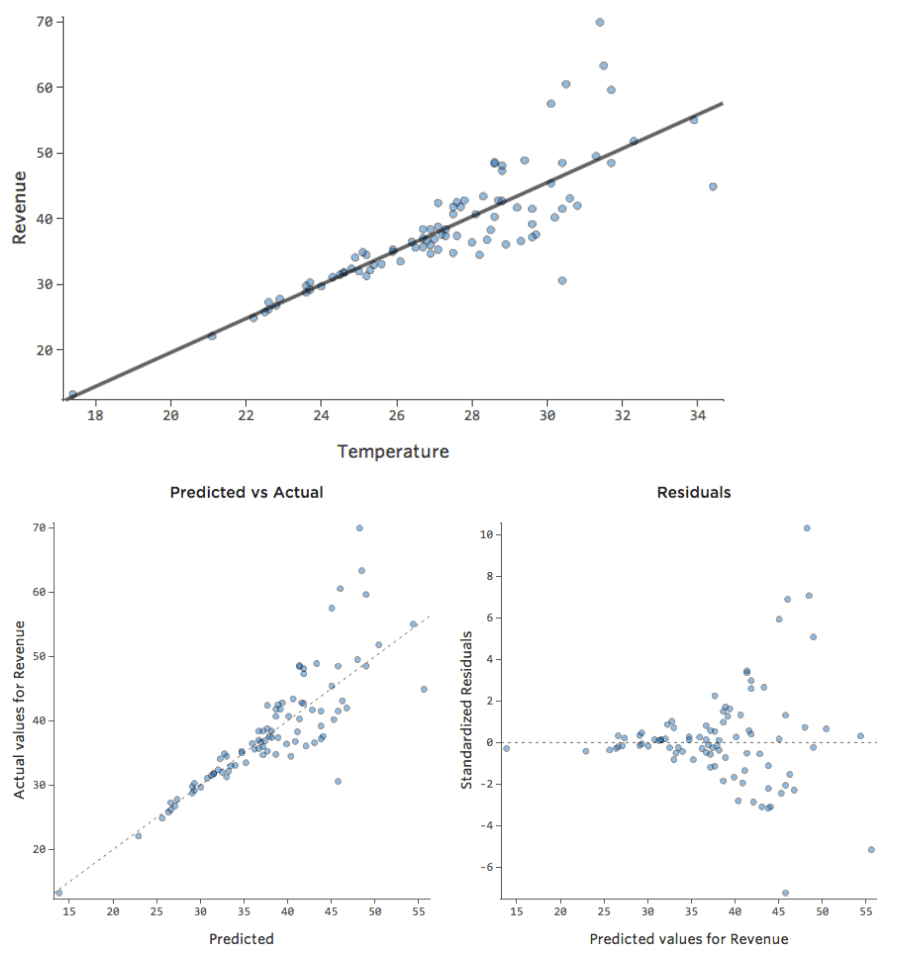
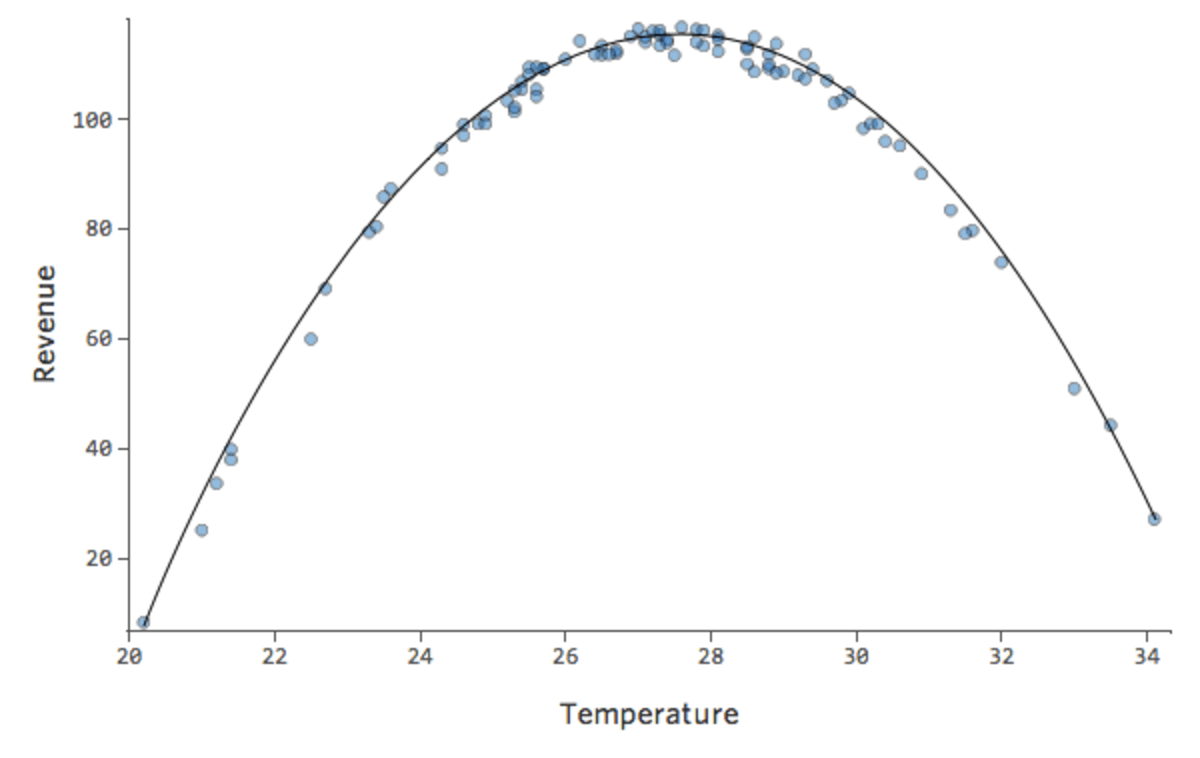
D’autres fois, un ajustement légèrement sous-optimal vous donnera quand même un bon aperçu de la relation, même s’il n’est pas parfait, comme ci-dessous :
Ce modèle semble assez précis. Si vous regardez attentivement (ou si vous regardez les résiduels), vous voyez qu’un modèle revient fréquemment ici : que les points sont sur une courbe à laquelle la ligne ne correspond pas vraiment.
Est-ce important ? C’est à vous de décider. Si vous obtenez une compréhension rapide de la relation, votre ligne droite représente une estimation assez correcte. Si vous utilisez ce modèle à des fins de prédiction et non d’explication, le modèle le plus précis possible prendra probablement compte de cette courbe.
Comment corriger le modèle ?
- Parfois, des modèles comme celui-ci indiquent qu’une variable doit être transformée.
- Si le modèle est en fait aussi clair que ces exemples, vous avez probablement besoin de créer un modèle non linéaire (ce n’est pas aussi difficile que cela paraît).
- Ou, comme toujours, il est possible que le problème soit une variable manquante.
Valeurs aberrantes
  ;
- Afficher les détails sur ce tracé et comment le corriger.
-
Problème
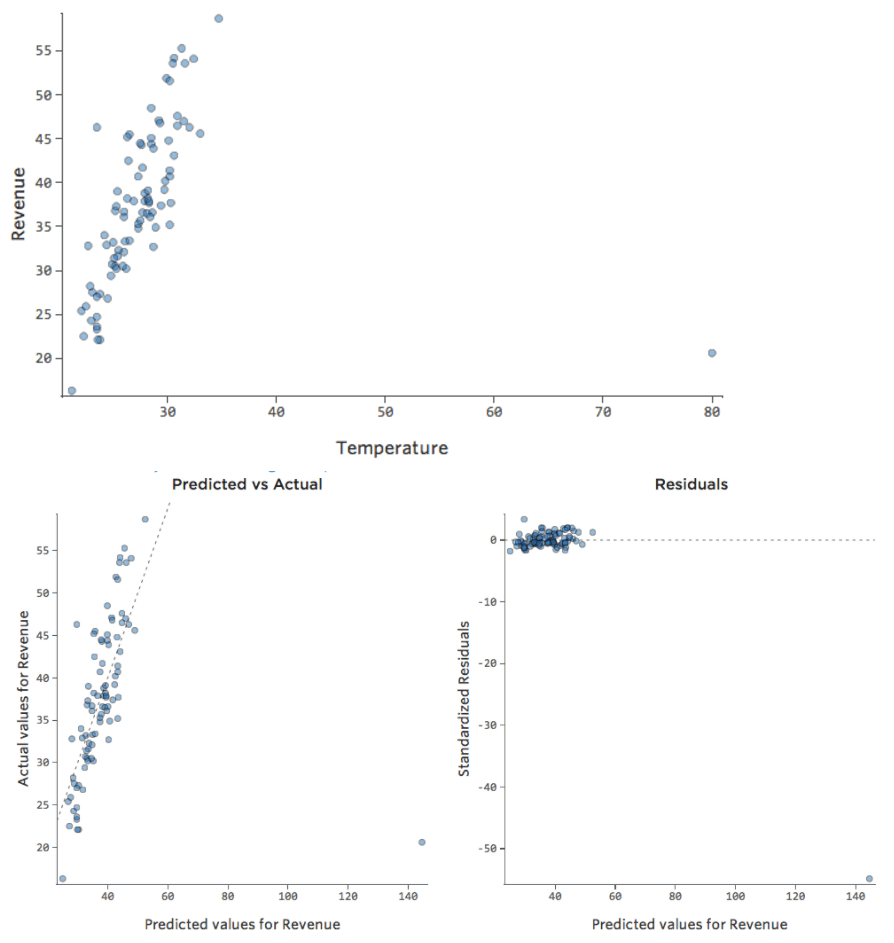
Et si l’un de vos points de données avait une « Température » de 80 au lieu des valeurs normales situées entre 20 et 30 ? Vos tracés ressembleraient à ceci :
Cette régression a un point de données aberrant sur une variable d’entrée, « Température » (les valeurs aberrantes sur une variable d’entrée sont également appelées « points de levier »).
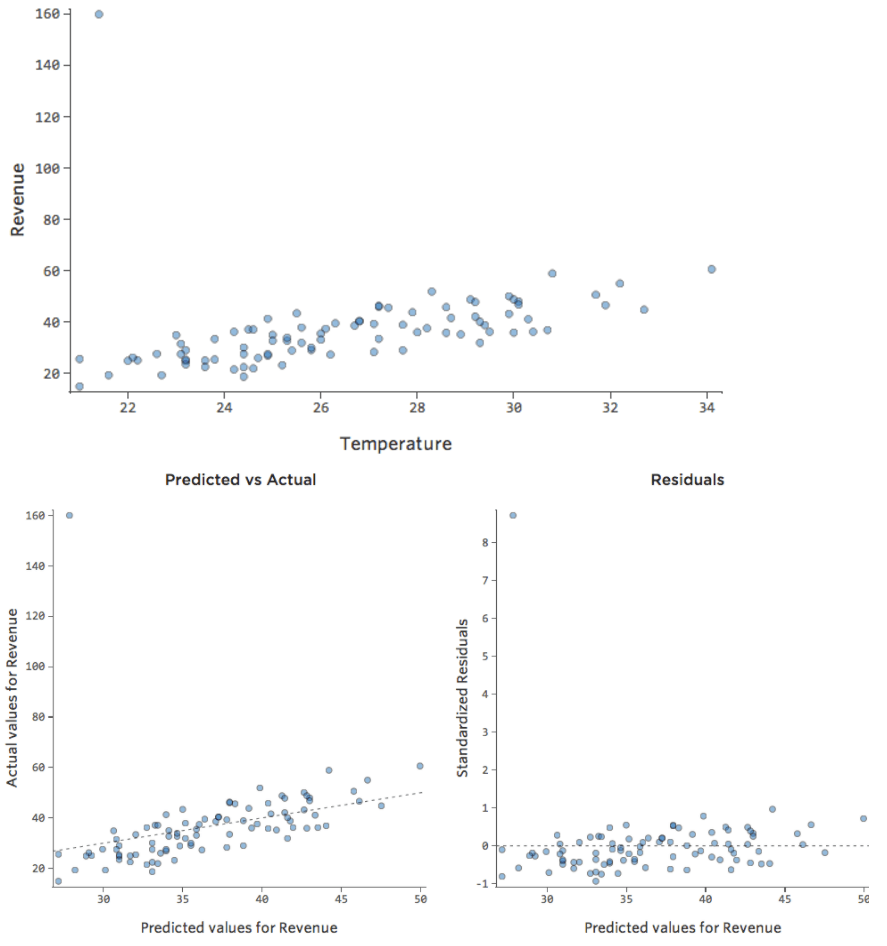
Et si l’un de vos points de données avait un Chiffre d’affaires de 160 USD au lieu d’une valeur entre 20 et 60 USD ? Vos tracés ressembleraient à ceci :
Cette régression a un point de données aberrant sur une variable de sortie, « Chiffre d’affaires ».
Conclusions
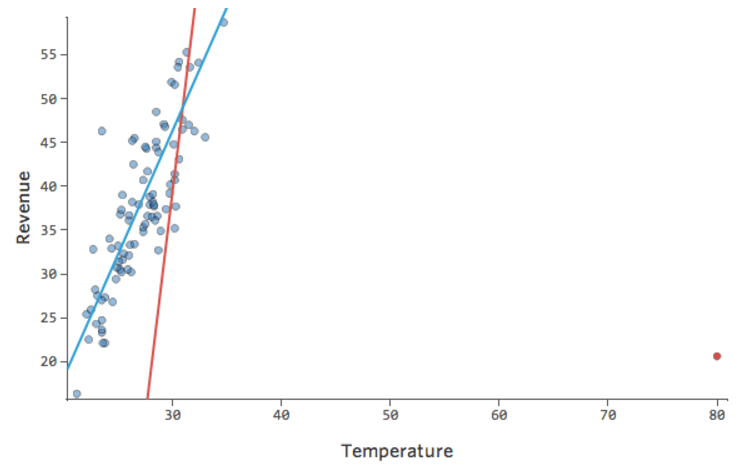
Stats iQ exécute un type de régression qui n’est généralement pas affecté par les valeurs aberrantes de sortie (comme le jour avec un « Chiffre d’affaires » de 160 USD), mais qui est affecté par les valeurs aberrantes d’entrée (comme une « Température » de 80). Dans le pire des cas, votre modèle peut pivoter pour essayer de se rapprocher de ce point au détriment d’être proche de tous les autres et d’être tout simplement faux, comme ceci :
Vous voudrez probablement avoir un modèle ressemblant à la ligne bleue. La ligne rouge quant à elle représente le modèle que vous pourriez avoir si vous avez cette valeur aberrante de « Temperature » à 80.
Comment corriger le modèle ?
- Il est possible qu’il s’agisse d’une erreur de mesure ou de saisie de données, et que la valeur aberrante soit simplement incorrecte, auquel cas vous devez la supprimer.
- Il est possible ces quelques valeurs aberrantes cachent en fait une distribution de la puissance. Envisagez de transformer la variable si l’une de vos variables a une distribution asymétrique (c’est-à-dire qu’elle n’a rien d’une forme de cloche).
- S’il s’agit d’une valeur aberrante légitime, vous devez évaluer l’impact de la valeur aberrante.
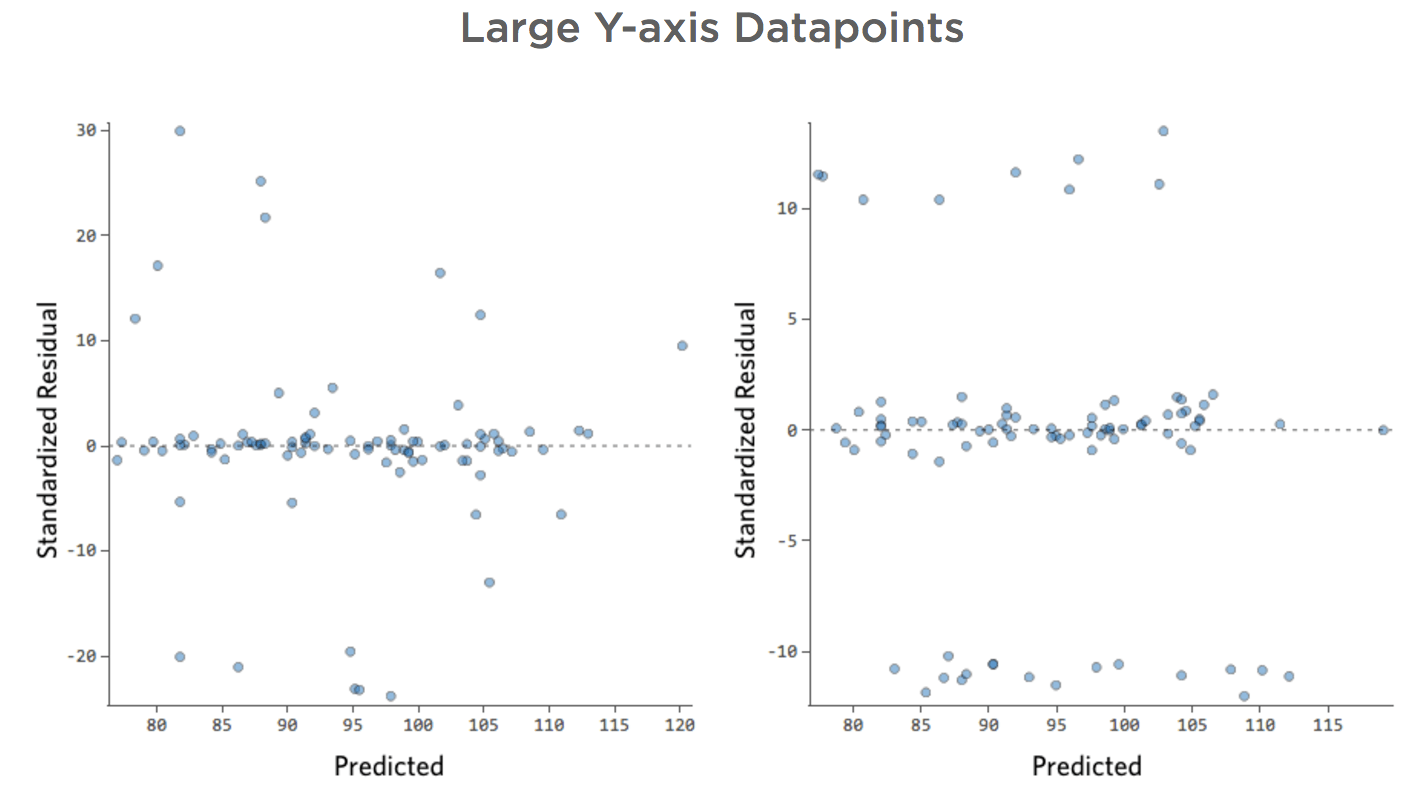
Points de données importants sur l’axe des ordonnées
- Afficher les détails sur ce tracé et comment le corriger.
-
Problème
Imaginez que deux stands de limonade concurrents opèrent à proximité du vôtre. La plupart du temps, un seul est opérationnel, auquel cas votre chiffre d’affaires est constamment bon. Parfois, ni l’un ni l’autre n’est actif et votre chiffre d’affaires s’envole ; à d’autres moments, les deux sont actifs et votre chiffre d’affaires chute.
“Chiffre d’affaires” vs. “Température” pourrait ressembler à ça…
…cette ligne du haut étant constituée des jours où aucun autre stand n’est présent et la ligne du bas correspond aux jours où les deux autres stands sont en activité.
Cela donnerait les tracés de résiduels suivants :
On a donc un certain nombre de points de données des deux côtés de 0 ayant des résiduels de 10 ou plus, c’est-à-dire que le modèle n’était pas du tout correct.
Maintenant, si vous aviez collecté des données chaque jour pour une variable appelée « Nombre de stands de limonade actifs », vous pourriez ajouter cette variable à votre modèle et ce problème serait corrigé. Cependant, vous n’avez pas souvent les données dont vous avez besoin (ou vous ne savez même pas de quel type de variable vous avez besoin).
Conclusions
Votre modèle n’est pas inutile, mais il n’est certainement pas aussi bon que si vous aviez toutes les variables dont vous aviez besoin. Vous pouvez toujours l’utiliser et vous vous dire quelque chose comme : « Ce modèle est assez précis la plupart du temps, mais il arrive qu’il ne soit pas du tout correct ». Est-ce utile ? Probablement, mais c’est à vous d’en décider et cela dépend des décisions que vous essayez de prendre en fonction de votre modèle.
Comment corriger le modèle ?
- Même si cette approche ne fonctionnerait pas dans l’exemple spécifique ci-dessus, il vaut presque toujours la peine de regarder autour pour voir s’il y a une opportunité de transformer utilement une variable.
- Si cela ne fonctionne pas, vous devrez probablement résoudre votre problème de variable manquante.
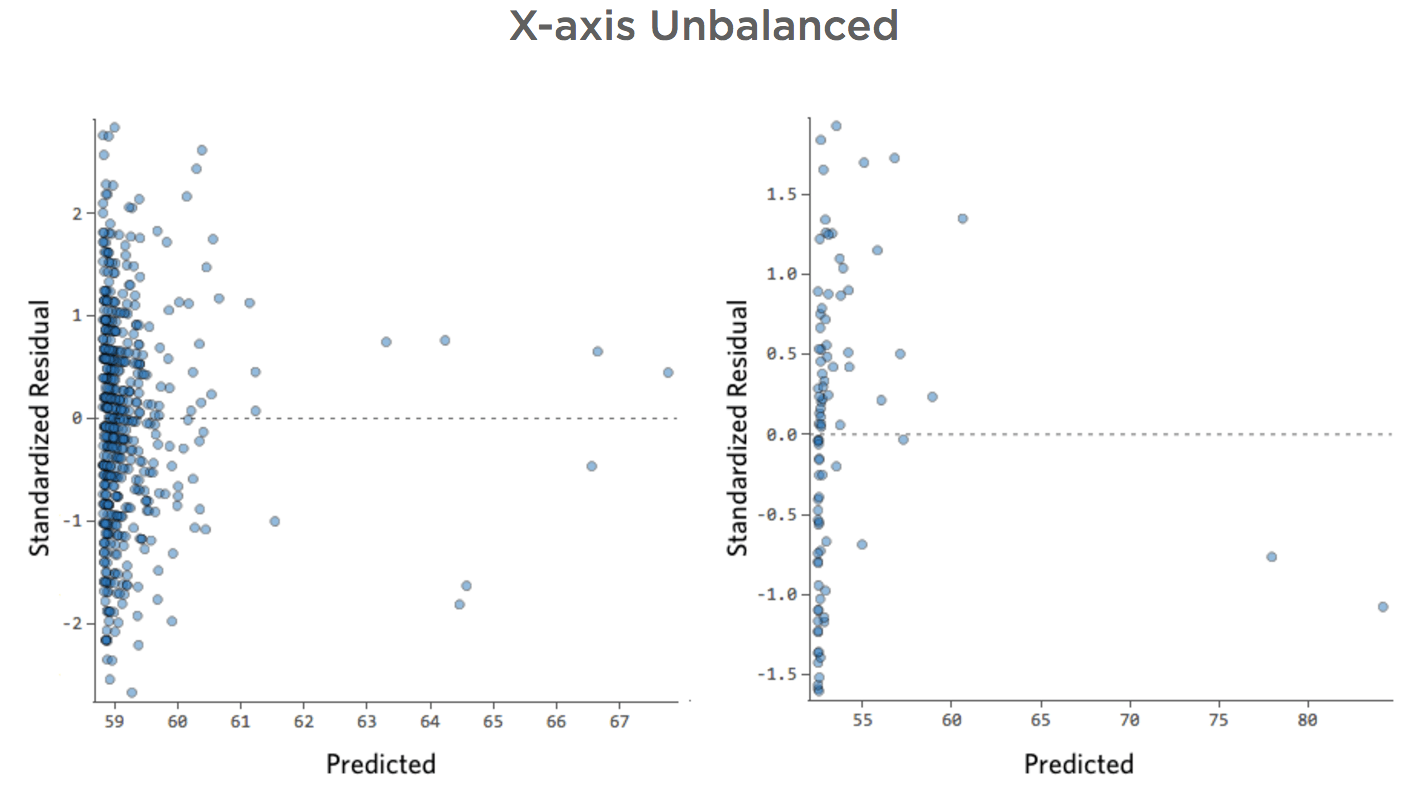
Axe des abscisses déséquilibré
  ;
- Afficher les détails sur ce tracé et comment le corriger.
-
Problème
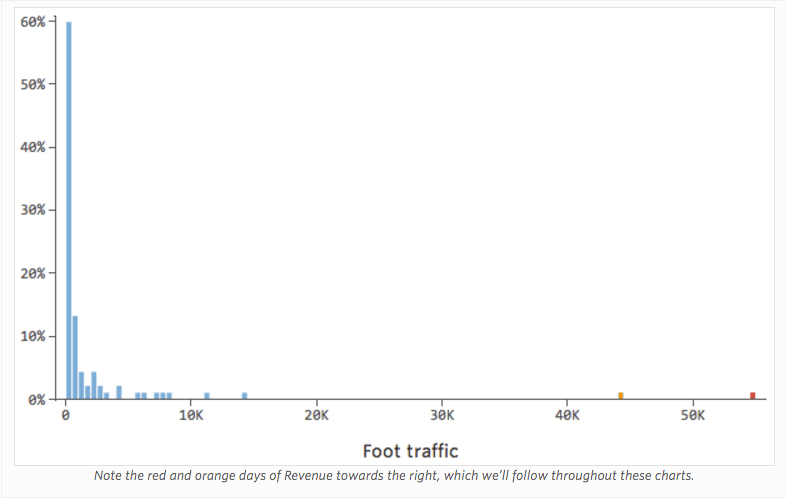
Imaginez que le « Chiffre d’affaires » est généré par la « Circulation piétonne » à proximité, en plus de la « Température » ou à la place de celle-ci. Imaginez que, pour une raison quelconque, votre stand de limonade a généralement un chiffre d’affaires bas, mais que de temps en temps vous avez des jours avec un chiffre d’affaires extrêmement élevé, de sorte que votre chiffre d’affaires ressemble à cela…
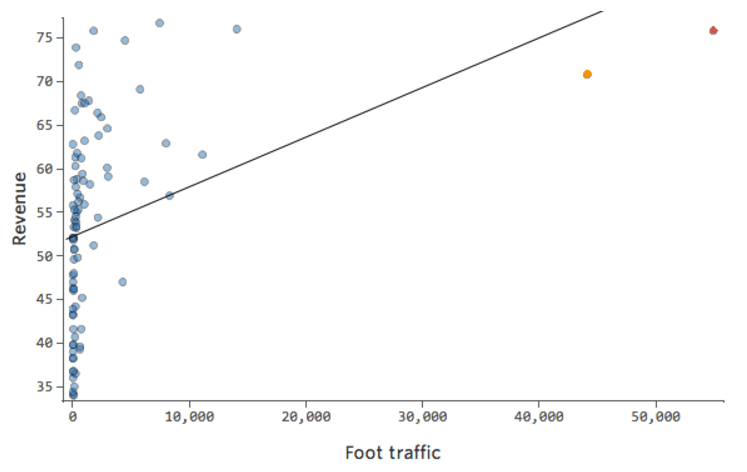
Donc Circulation piétonne vs. Chiffre d’affaires pourrait ressembler à cela, la plupart des données étant regroupées sur le côté gauche :
La ligne noire représente l’équation du modèle, la prédiction du modèle du lien entre « Circulation piétonne » et « Chiffre d’affaires ». Vous pouvez voir que le modèle ne fait pas vraiment la différence entre une « Circulation piétonne » de 0 et de 100 ou 1 000 ; pour chacune de ces valeurs, il estimerait un chiffre d’affaires proche de 53 USD.
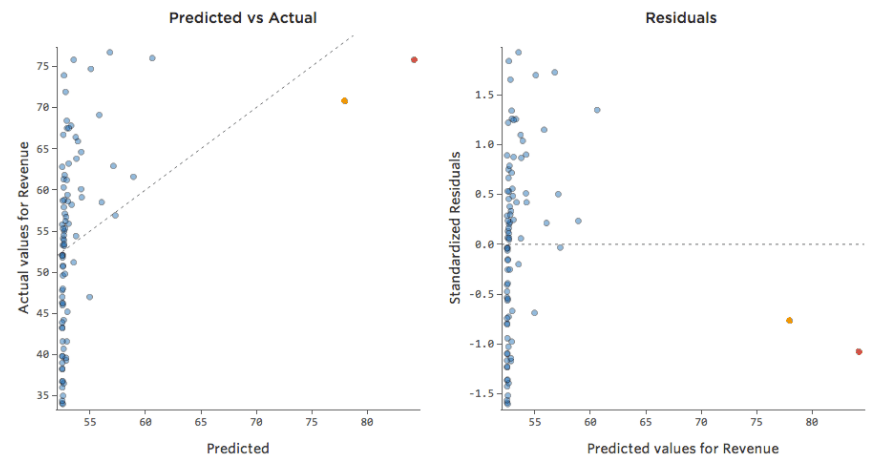
Voici les mêmes données traduites en tracés de diagnostic :
Conclusions
Parfois, votre modèle ne présente en fait aucun problème. Dans l’exemple ci-dessus, il est assez clair qu’il ne s’agit pas d’un bon modèle, mais parfois le tracé résiduel est déséquilibré et le modèle est assez bon.
Les seules façons de savoir si le modèle est bon sont les suivantes : a) tenter de transformer vos données et voir si vous pouvez améliorer le modèle et b) examiner le tracé Prédit vs. Réel et voir si votre prédiction est complètement fausse pour beaucoup de points de données, comme dans l’exemple ci-dessus (mais contrairement à l’exemple ci-dessous).
Bien qu’il n’y ait pas de règle explicite démontrant qu’un résiduel ne peut pas être déséquilibré et quand même précis (ce modèle est en effet assez précis), bien souvent, le fait est qu’un résiduel avec un axe des abscisses déséquilibré signifie que votre modèle peut être rendu significativement plus précis. La plupart du temps, vous constaterez que le modèle était correct sur le plan directionnel, mais assez inexact par rapport à une version améliorée. Il n’est pas rare de résoudre un problème comme celui-ci et, par conséquent, de voir le coefficient de détermination du modèle passer de 0,2 à 0,5 (sur une échelle de 0 à 1).
Comment corriger le modèle ?
- La solution consiste presque toujours à transformer vos données, généralement une variable de réponse. (Notez que l’exemple ci-dessous fera référence à la transformation de votre variable de réponse, mais le même processus sera utile ici.)
- Il est également possible qu’une variable manque à votre modèle.
Amélioration de votre modèle : évaluation de l’impact d’une valeur aberrante
Supposons que vous avez un point de données aberrant légitime, et non une erreur de mesure ou de données. Pour décider de la marche à suivre, vous devez évaluer l’impact du point de données sur la régression.
La manière la plus simple de procéder est de noter les coefficients de votre modèle actuel, puis de filtrer ce point de données à partir de la régression. Si le modèle ne change pas beaucoup, alors vous n’avez pas vraiment à vous inquiéter.
Si cela modifie le modèle de manière significative, examinez le modèle (en particulier Prédit vs. Réel) et décidez lequel vous semble le plus adapté. Il est acceptable d’éliminer la valeur aberrante du moment que vous pouvez théoriquement justifier, par exemple : « Dans ce cas, nous ne sommes pas intéressés par les valeurs aberrantes, elles ne sont pas importantes. » ou « C’est le jour où oncle Jerry est venu acheter de la limonade et m’a donné 100 USD ; ce n’est pas prévisible et cela ne vaut pas la peine d’être inclus dans le modèle. »
Amélioration de votre modèle : transformation des variables
Aperçu
La manière la plus courante d’améliorer un modèle consiste à transformer une ou plusieurs variables, généralement à l’aide d’une transformation logarithmique ou « log ».
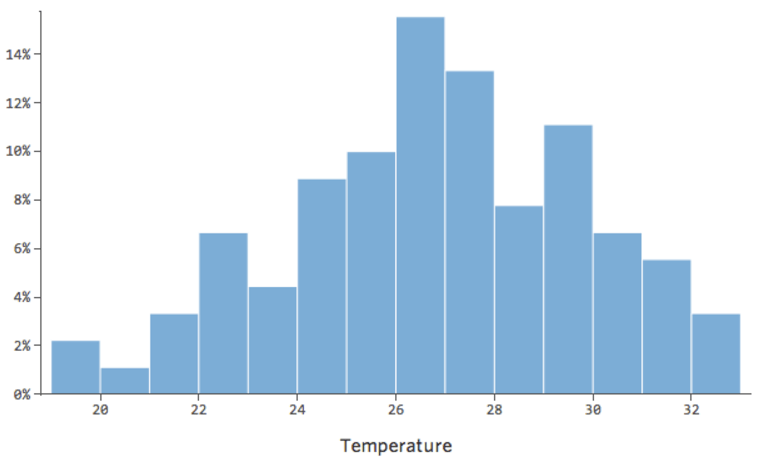
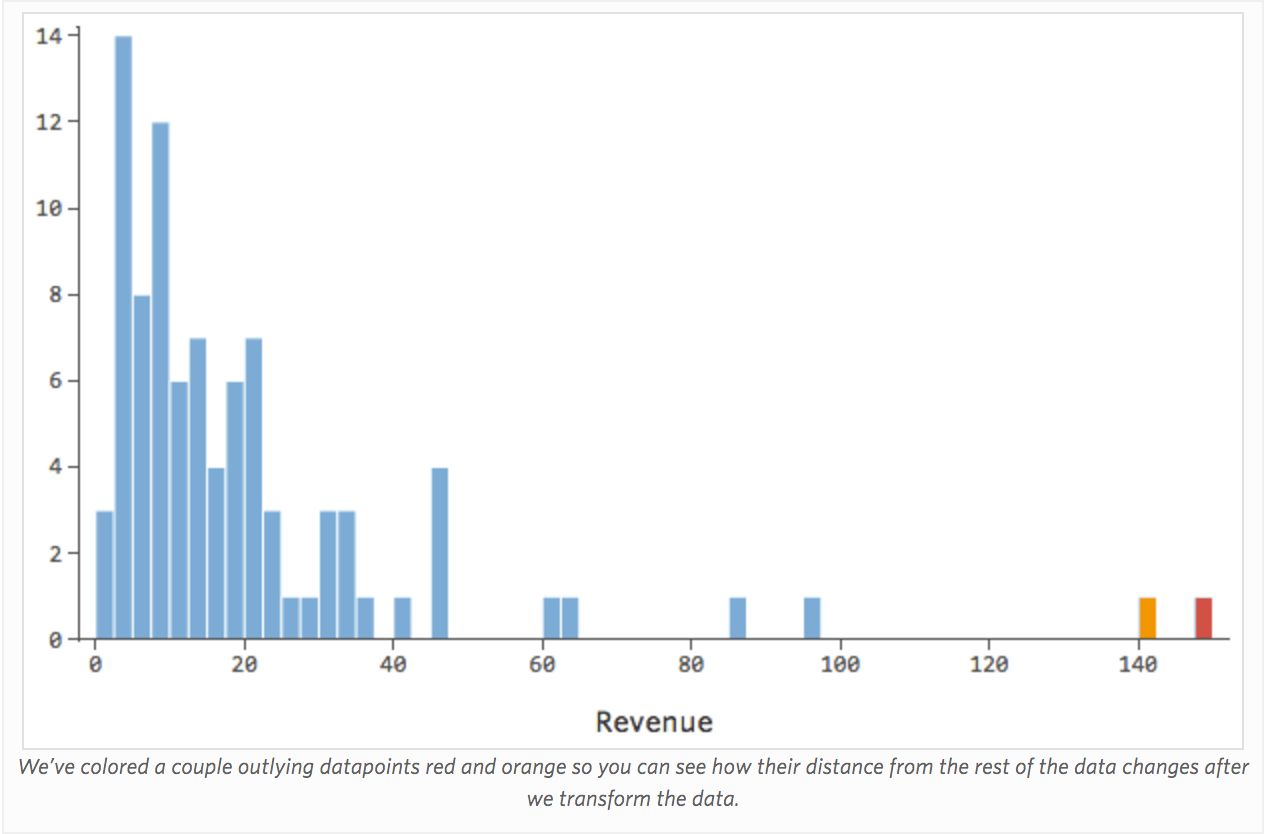
La transformation d’une variable modifie la forme de sa distribution. Typiquement le meilleur endroit pour commencer est une variable qui a une distribution asymétrique, par opposition à une distribution plus symétrique ou en forme de cloche. Il vous faut trouver une variable comme celle-ci à transformer :
En général, les modèles de régression fonctionnent mieux avec des courbes plus symétriques, en forme de cloche. Essayez différents types de transformations jusqu’à ce que vous atteigniez celui qui est le plus proche de cette forme. Il n’est souvent pas possible d’obtenir cette forme, mais l’objectif est de s’en rapprocher. Imaginons donc que vous preniez la racine carrée du « Chiffre d’affaires », afin d’obtenir une forme plus symétrique, et que votre distribution ressemble à ceci :
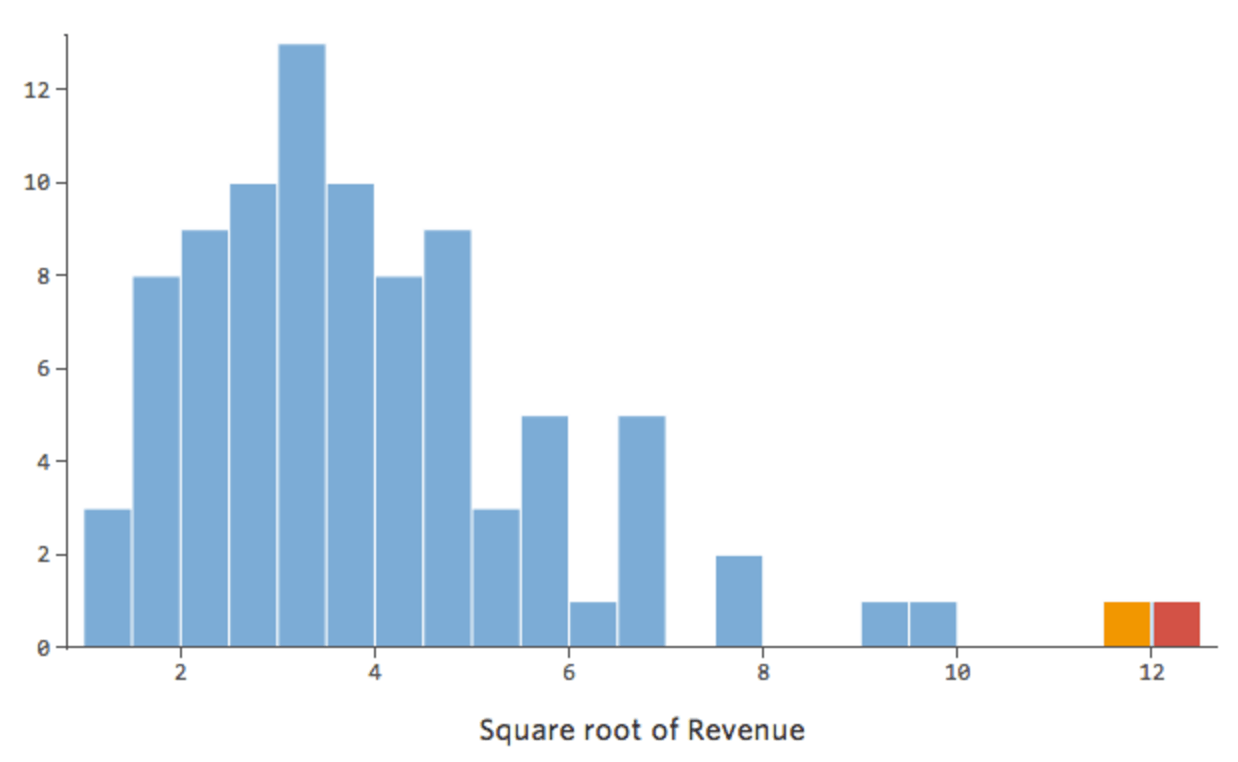
C’est bien, mais c’est encore un peu asymétrique. Essayons plutôt de prendre le log de « Chiffre d’affaires », qui donne cette forme :
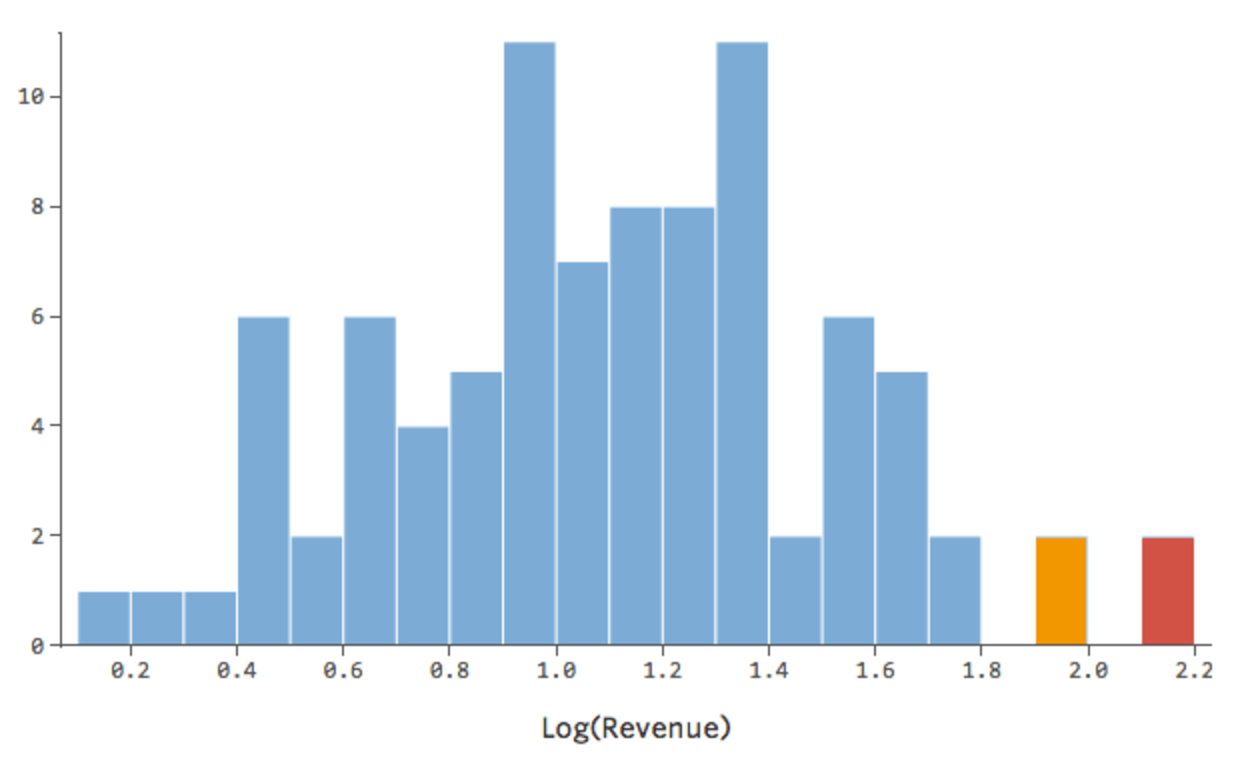
C’est bien et c’est symétrique. Vous obtiendrez probablement un meilleur modèle de régression avec log (« Chiffre d’affaires ») qu’avec « Chiffre d’affaires ». En effet, voici comment votre équation, vos résiduels et votre coefficient de détermination pourraient changer :
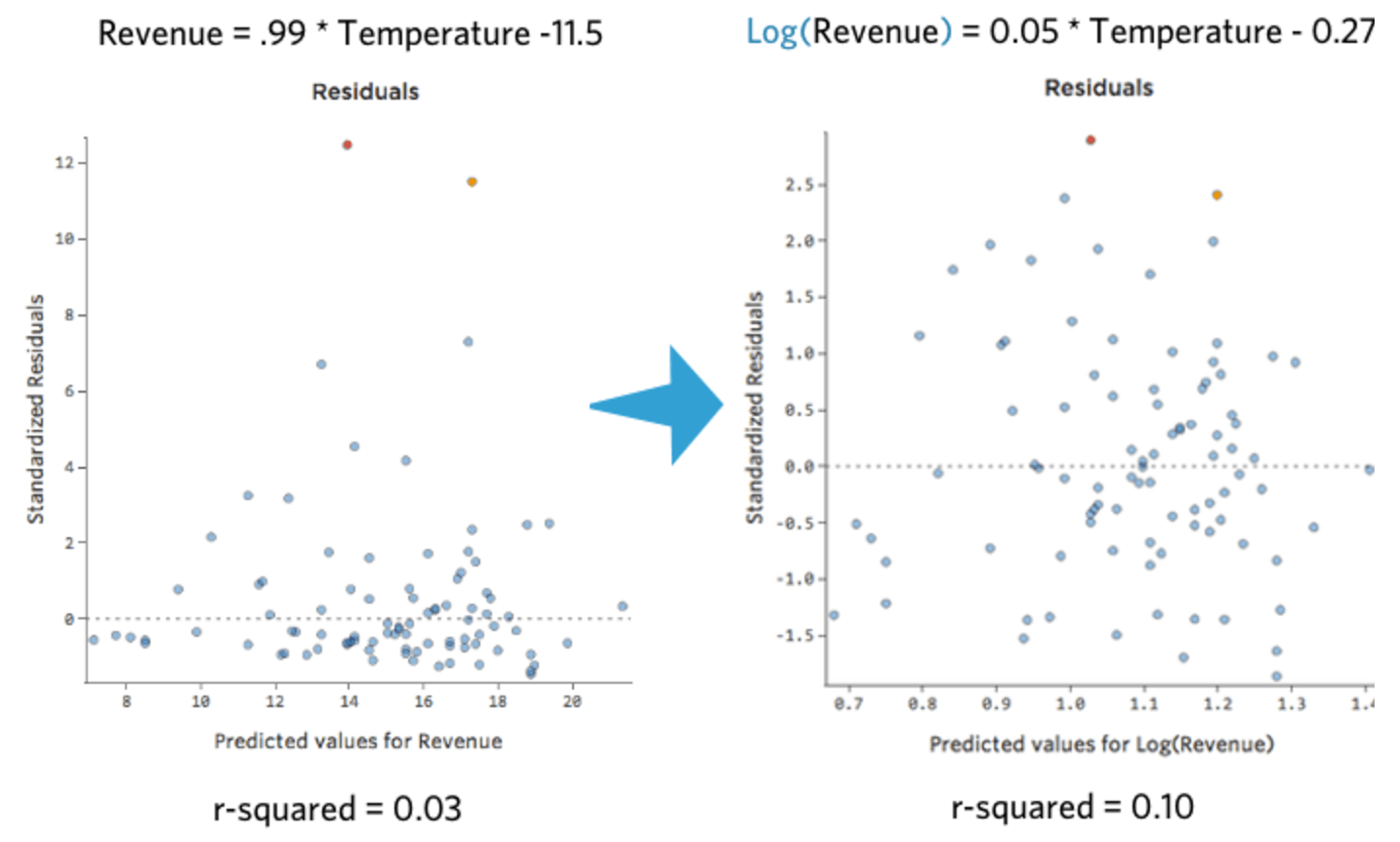
Stats iQ affiche une petite version de la distribution de la variable conformément à ‘équation de régression :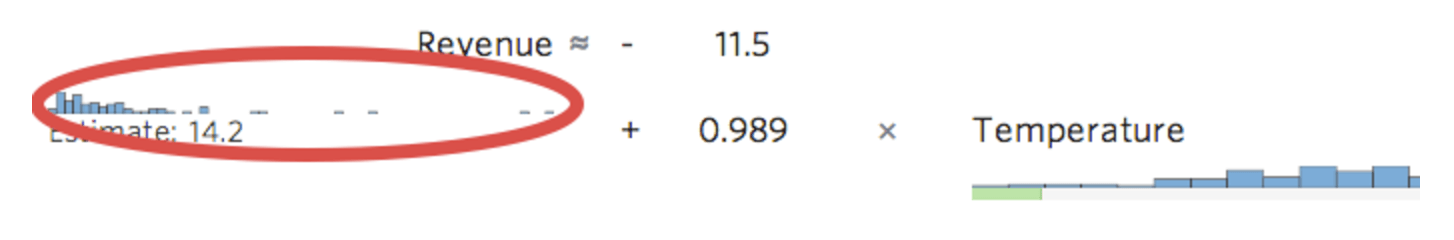
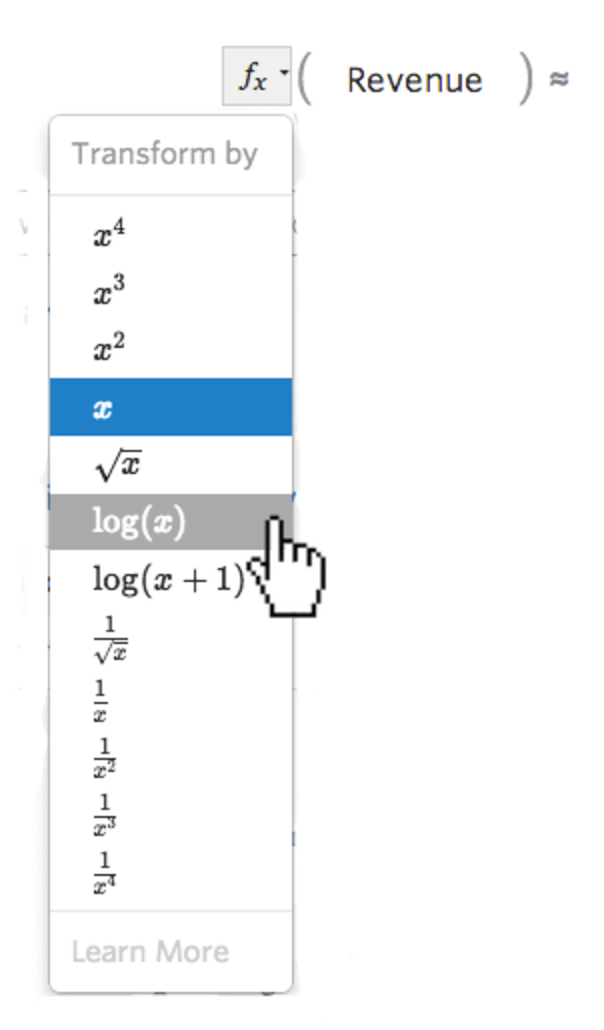
Sélectionnez le bouton de transformation fx à gauche de la variable…
… puis sélectionnez une transformation, le plus souvent log(x)...
…puis examinez l’histogramme pour voir s’il est plus centré, car celui-ci est postérieur à la transformation :

Après avoir transformé une variable, notez comment sa distribution, le coefficient de détermination de la régression et les schémas du tracé de résidus changent. Si ceux-ci s’améliorent (en particulier le coefficient de détermination et les résidus), il est probablement préférable de conserver la transformation.
Si une transformation est nécessaire, vous devez commencer par une transformation « log » car les résultats de votre modèle seront toujours faciles à comprendre. Cependant, remarquez que vous rencontrerez des problèmes si les données que vous essayez de transformer incluent des zéros ou des valeurs négatives. Pour savoir pourquoi il est si utile d’utiliser Log, si vous vous souhaitez transformer des chiffres non positifs ou si vous voulez simplement mieux comprendre ce qui se passe lorsque vous transformez des données, lisez les détails ci-dessous.
Détails
Si vous prenez le log10() d’un nombre, vous dites « 10 à la puissance qui me donne ce nombre ». Par exemple, voici un tableau simple de quatre points de données, incluant à la fois « Chiffre d’affaires » et Log (« Chiffre d’affaires ») :
| Température | Chiffre d’affaires | Log(Chiffre d’affaires) |
|---|---|---|
| 20 | 100 | 2 |
| 30 | 1 000 | 3 |
| 40 | 10 000 | 4 |
| 45 | 31 623 | 4,5 |
Notez que si nous traçons la « Température » par rapport au « Chiffre d’affaires » et la « Température » par rapport au Log(« Chiffre d’affaires »), ce dernier modèle s’adapte beaucoup mieux.
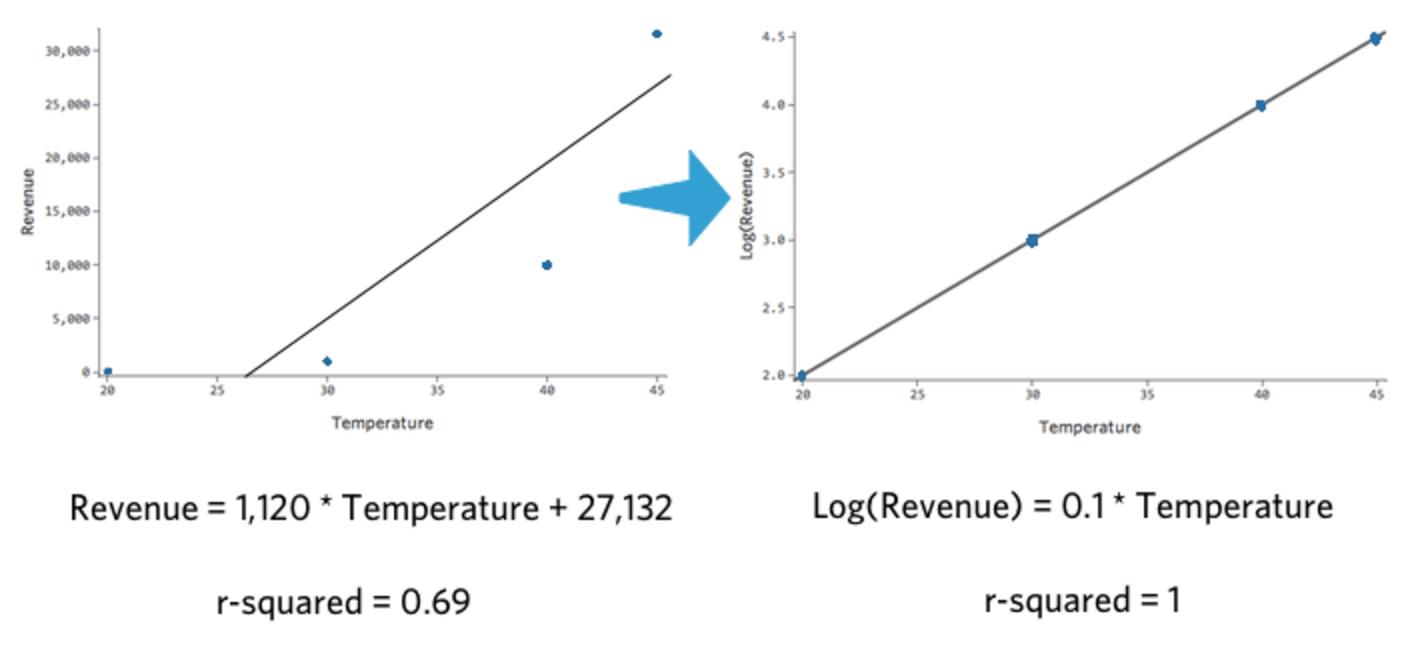
Ce qui est intéressant à propos de cette transformation, c’est que votre régression n’est plus linéaire. Lorsque la « Température » est passée de 20 à 30, le « Chiffre d’affaires » est passé de 10 à 100, un écart de 90 unités. Ensuite, lorsque la « Température » est passée de 30 à 40, le « Chiffre d’affaires » est passé de 100 à 1 000, soit un écart beaucoup plus important.
Si vous avez pris un logarithme de votre variable de réponse, il n’est plus vrai qu’une augmentation d’une unité de la « Température » signifie une augmentation de X unités du « Chiffre d’affaires ». Maintenant, c’est une augmentation de X pour cent du « Revenu ». Dans ce cas, une augmentation de dix unités de « Température » est associée à une augmentation de 1 000 % de Y, c’est-à-dire qu’une augmentation d’une unité de la « Température » est associée à une augmentation de 26 % du « Chiffre d’affaires ».
Notez également que vous ne pouvez pas prendre le logarithme de 0 ou d’un nombre négatif (il n’y a pas de X où 10X = 0 ou 10X= -5), donc si vous effectuez une transformation logarithmique, vous perdrez ces points de données de la régression. Il existe 4 façons courantes de gérer la situation :
- Prenez une racine carrée, ou une racine cube. Ces valeurs ne modifieront pas la forme de la courbe aussi radicalement qu’en utilisant un log, mais elles permettent aux zéros de rester dans la régression.
- S’il n’y a pas trop de lignes de données dont la valeur est zéro, et que ces lignes ne sont théoriquement pas importantes, vous pouvez continuer avec le log et perdre quelques lignes de votre régression.
- Au lieu d’utiliser log(y), utilisez log(y+1), de sorte que les zéros deviennent des uns et peuvent ensuite être conservés dans la régression. Cette technique biaise légèrement votre modèle et est quelque peu mal vue, mais dans la pratique, ses effets secondaires négatifs sont généralement assez mineurs.
Amélioration de votre modèle : variables manquantes
La raison la plus courante pour laquelle un modèle ne correspond pas est que toutes les variables appropriées ne sont pas incluses. Ce problème particulier a beaucoup de solutions possibles.
Ajouter une nouvelle variable
Parfois, l’ajout d’une autre variable suffit à corriger le modèle. Par exemple, si le trafic « Chiffre d’affaires » du stand de limonade était beaucoup plus important le week-end que les jours de la semaine, votre tracé Prédit vs. Réel pourrait ressembler à ce qui suit (avec un coefficient de détermination de 0,053) puisque le modèle ne prend que la moyenne des jours de week-end et des jours de la semaine :
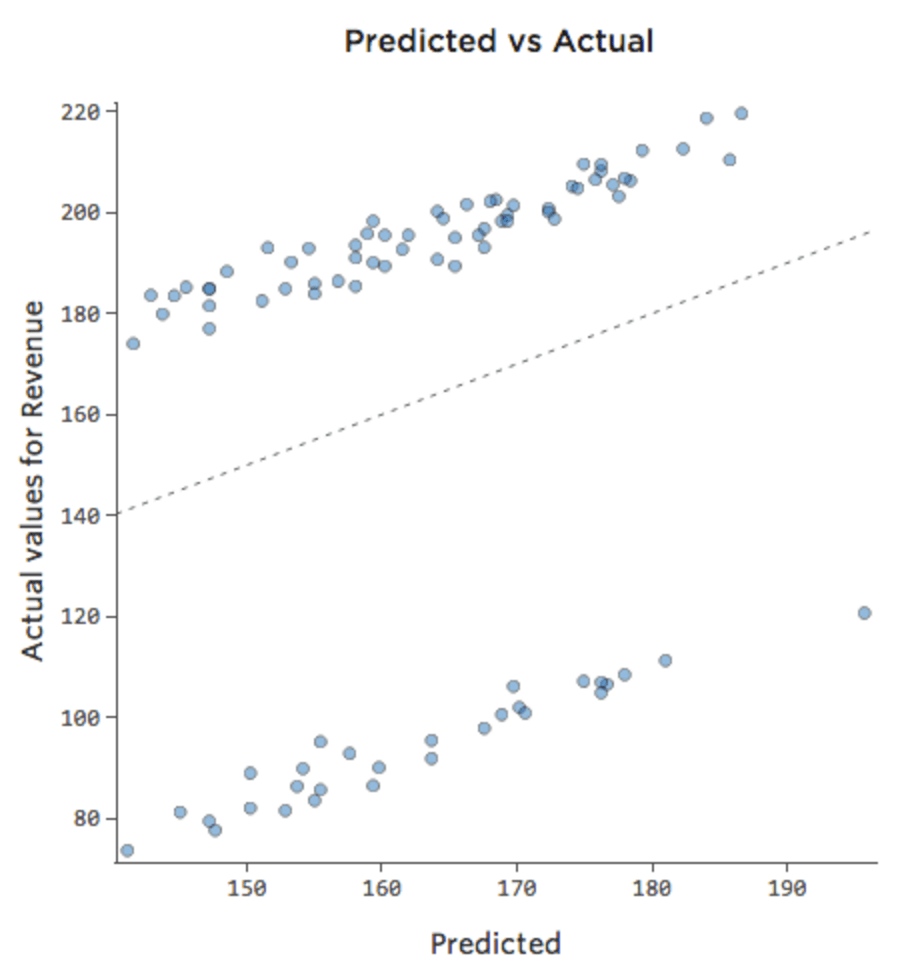
Si le modèle inclut une variable appelée « Week-end », alors le tracé Prédit vs. Réel pourrait ressembler à cela (avec un coefficient de détermination de 0,974) :
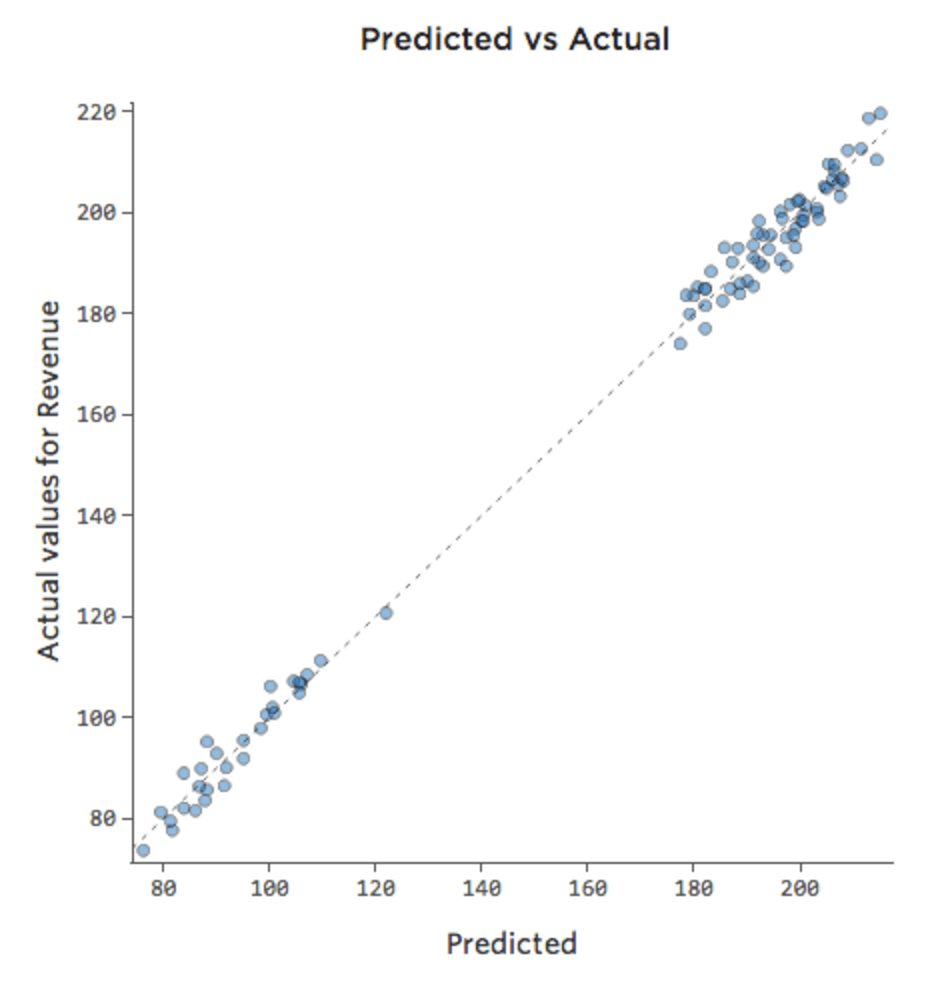
Le modèle effectue des prédictions beaucoup plus précises, car il est capable de prendre en compte si un jour est un jour de la semaine ou du week-end.
Remarquez que vous devrez parfois créer des variables dans Stats iQ pour améliorer votre modèle de cette manière. Par exemple, vous avez peut-être une variable « Date » (avec des valeurs comme « 10/26/2014 ») et il vous faudra peut-être créer une nouvelle variable appelée « Jour de la semaine » (c.-à-d. dimanche) ou Week-end (c.-à-d. week-end).
Variable omise non disponible
Mais c’est rarement si facile. Très souvent, la variable pertinente n’est pas disponible car vous ne savez pas de quoi il s’agit ou parce qu’elle était difficile à collecter. Peut-être que le problème ne venait pas du jour de la semaine, mais plutôt du « Nombre de concurrents dans la zone » que vous n’avez pas pu collecter sur le moment.
Si la variable dont vous avez besoin n’est pas disponible, ou si vous ne savez même pas quelle variable est manquante, alors votre modèle ne peut pas vraiment être amélioré et vous devez l’évaluer et décider dans quelle mesure vous êtes satisfait (s’il est utile ou non, même défectueux).
Interactions entre variables
Peut-être que le stand de limonade vend toujours à 100 % de sa capacité le week-end, et donc le « Chiffre d’affaires » est élevé, quelle que soit la « Température ». Mais en semaine, le stand de limonade est beaucoup moins actif, donc « Température » est un moteur important de « Revenus ». Si vous avez exécuté une régression qui incluait « Week-end » et « Température », vous pourriez voir un tracé Prédit vs. Réel comme celui-ci, où la rangée le long du haut correspond aux jours de week-end.
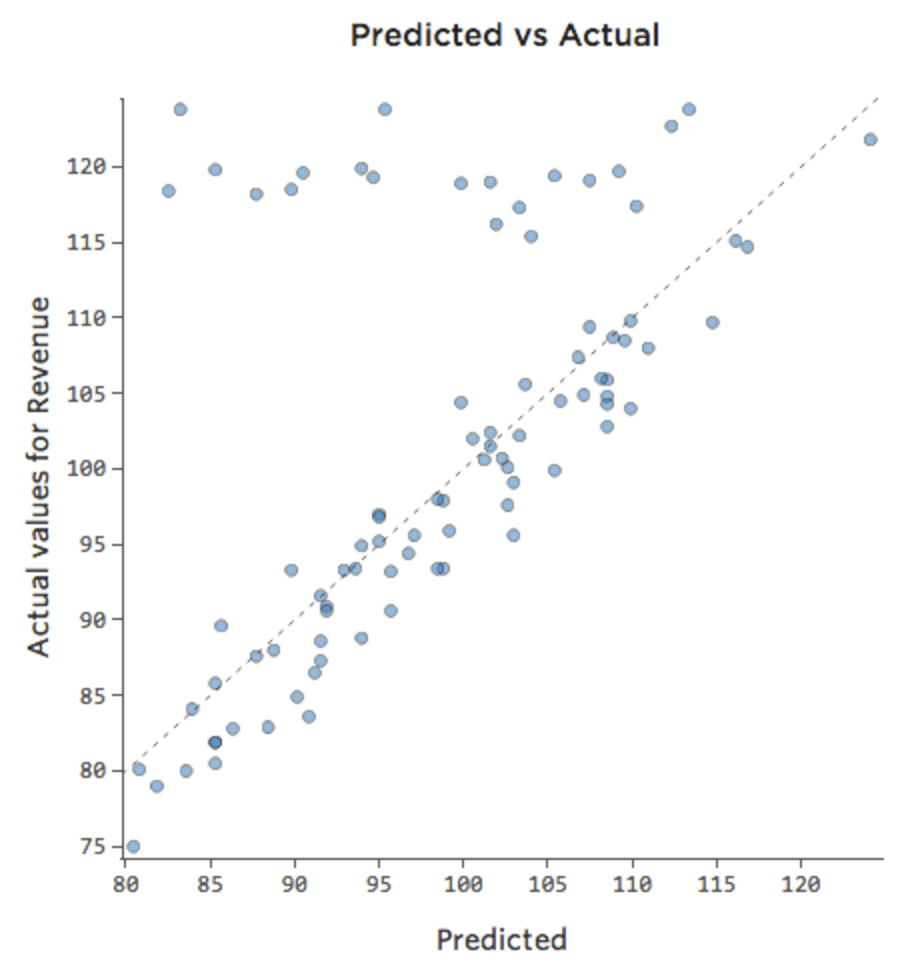
On dira alors qu’il y a une interaction entre le « Week-end » et la « Température »; l’effet de l’un d’eux sur le « Chiffre d’affaires » est différent en fonction de la valeur de l’autre. Si nous créons une variable d’interaction, nous obtenons un modèle bien meilleur, qui fournit un tracé Prédit vs. Réel ressemblant à ceci :
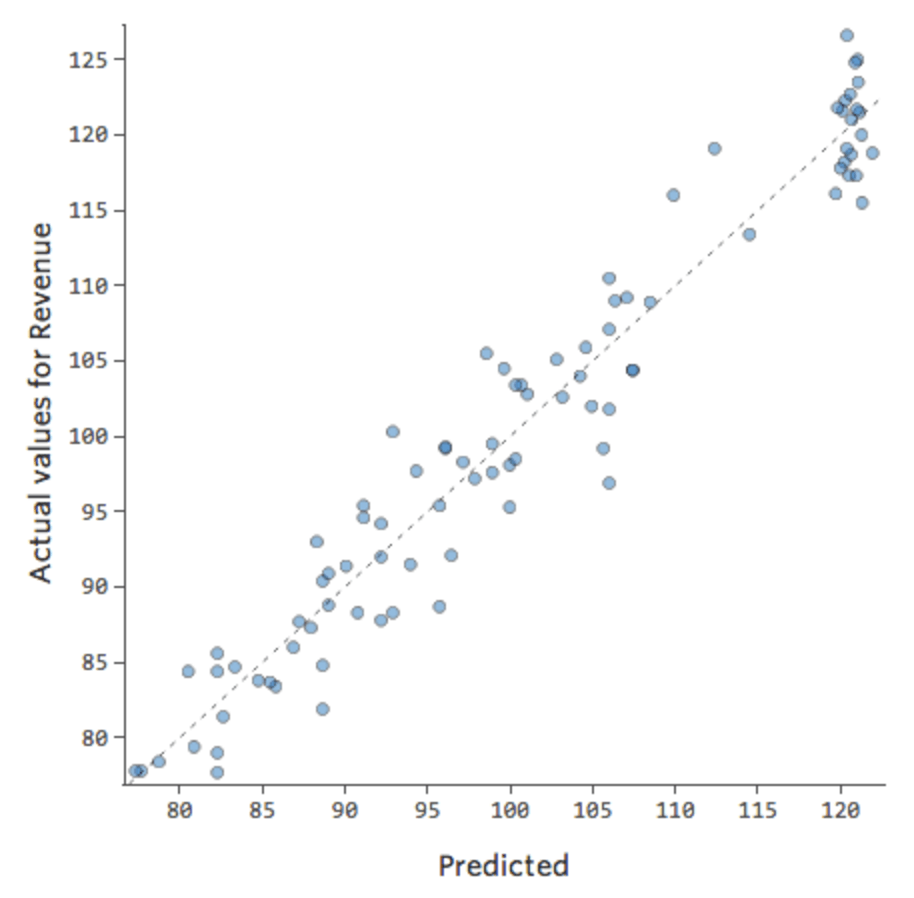
Amélioration de votre modèle : résolution de la non-linéarité
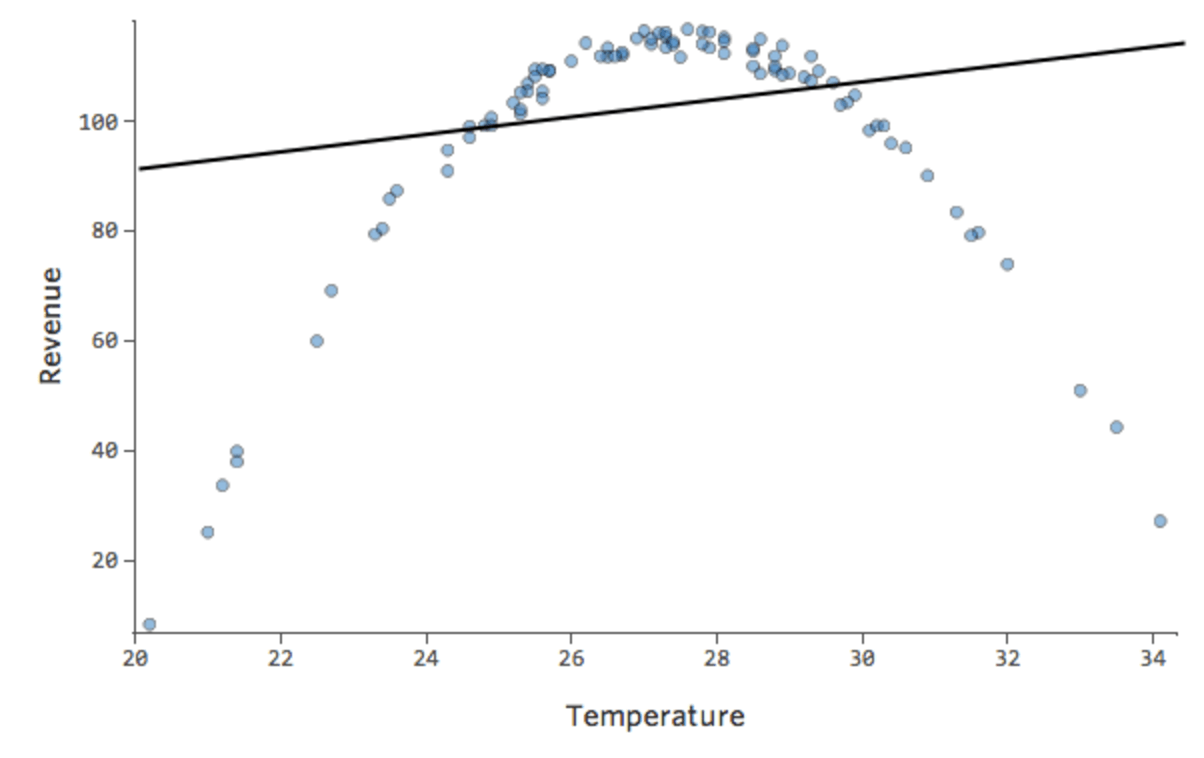
Imaginons que vous ayez une relation qui ressemble à ceci :
Vous remarquerez peut-être que la forme est celle d’une parabole, dont vous pouvez vous rappeler qu’elle est généralement associée à des formules qui ressemblent à ceci :
y = x2 + x + 1
Par défaut, la régression utilise un modèle linéaire qui ressemble à ceci :
y = x + 1
En fait, la ligne dans le tracé ci-dessus a cette formule :
y = 1,7x + 51
Mais c’est un ajustement très sous-optimal. Donc si nous ajoutons un terme x2, notre modèle a une meilleure chance de correspondre à la courbe. En fait, cela crée ceci :
La formule pour cette courbe est la suivante :
y = – 2x2 + 111x – 1408
Cela veut dire que nos tracés diagnostiques changent, passant de ça…
… à ça :
Notez qu’il s’agit de tracés diagnostiques sains, même si les données semblent être déséquilibrées sur le côté droit.
L’approche ci-dessus peut être étendue à d’autres types de formes, en particulier une courbe en forme de S, en ajoutant un terme x3. C’est relativement peu fréquent, cependant.
Quelques mises en garde :
- D’une manière générale, si vous avez terme x2 en raison d’un motif non linéaire dans vos données, vous voulez avoir un terme x-simple-ancien-non-x2. Vous constaterez peut-être que votre modèle est parfaitement bon sans ce terme, mais vous devriez certainement essayer les deux pour commencer.
- L’équation de régression peut être difficile à comprendre. Pour l’équation linéaire au début de cette section, pour chaque unité supplémentaire de « Température », « Chiffre d’affaires » a augmenté de 1,7 unité. Lorsque vous avez à la fois x2 et x dans l’équation, il n’est pas facile de dire « Lorsque la température augmente d’un degré, voici ce qui se passe. » Parfois, pour cette raison, il est plus facile d’utiliser simplement une équation linéaire, en supposant que cette équation fonctionne suffisamment bien.